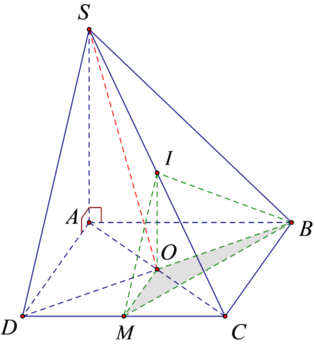
Cho hình chóp S.ABCD có đáy là hình vuông tâm O, SA vuông góc với đáy ABCD. Gọi I là trung điểm của SC. Xét các khẳng định sau:
1. O I ⊥ ( A B C D ) 2. A C ⊥ ( S B D ) 3. I A = I B = I C = I D 4. B C ⊥ S C D
A. 3
B. 1
C. 4
D. 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Do IO là đường trung bình của tam giác SAC nên:
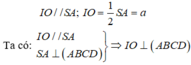
* OM là đường trung bình tam giác ACD nên:
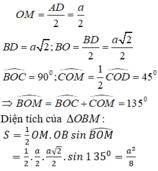
Tính thể tích của khối chóp I.OBM:
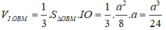

Đề bài sai rồi bạn
Muốn HK song song BD thì H, K phải là hình chiếu của A lên SB và SD

Chọn D.
Vì S A ⊥ ( A B C D ) nên AC là hình chiếu vuông góc của SC lên(ABCD).
Góc giữa giữa SC và mp (ABCD) bằng góc SC&AC ⇒ α = SCA.
Xét tam giác SAC vuông tại A có
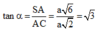
⇒ α = 60 o

Vì S A ⊥ A B C D nên AC là hình chiếu vuông góc của SC lên (ABCD).
Góc giữa giữa SC và mp (ABCD) bằng góc SC&AC ⇒ α = SCA.
Xét tam giác SAC vuông tại A có
tan α = S A A C = a 6 a 2 = 3 ⇒ α = 60 o
Chọn D
Đáp án D
Vì O,I lần lượt là trung điểm của AC,SC. Suy ra OI//SA mà S A ⊥ A B C D ⇒ O I ⊥ A B C D .
S A ⊥ A B C D ⇒ S A ⊥ B D mà B D ⊥ A C ⇒ B D ⊥ S A C .
Ta có S A ⊥ C D A D ⊥ C D ⇒ C D ⊥ S A D ⇒ C D ⊥ S D ⇒ ∆ S C D vuông tại D.
Suy ra ID = IC tương tự ta được I B = I C ⇒ I A = I B = I C = I D .
BC không vuông góc với mặt phẳng (SCD) vì S C B ^ < 90 °
Vậy có hai khẳng định đúng là 1 và 3.