Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
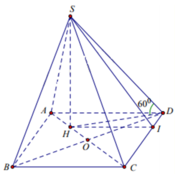
Gọi I ∈ C D sao cho H I / / A D .
Ta có H I A D = C H C A ⇔ H I = A D . C H C A = 2 a . 3 4 = 3 a 2 .
Và H D = D O 2 + H O 2 = D O 2 + D O 2 4 = D O 5 2 .
Mà 2 D O 2 = 4 a 2 ⇒ D O = a 2
⇒ H D = a 2 . 5 2 = a 10 2 ⇒ S H = H D . tan 60 ∘ = a 30 2 .
Vậy α = S I H ^ ⇒ tan α = S H H I = a 30 2 3 a 2 = 30 2 .

Phương pháp:
- Sử dụng phương pháp tọa độ trong không gian, gắn hệ trục tọa độ gốc A và các trục tọa độ sao cho

- Sử dụng các công thức điểm, véc tơ, mặt phẳng, góc giữa hai mặt phẳng để tính toán.
Cách giải:
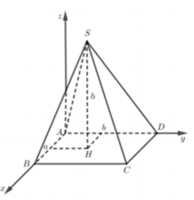
Gắn hệ trục tọa độ như hình vẽ, giả sử ABCD là hình vuông cạnh l,
chiều cao hình chóp SH = h.
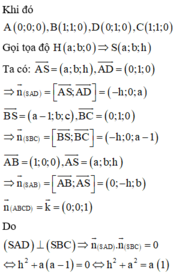
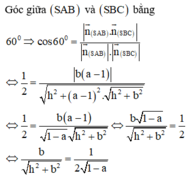
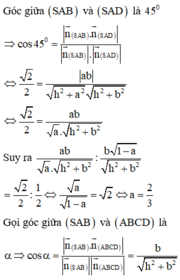
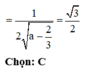

Đáp án A
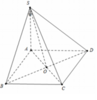
Ta có C B ⊥ A B C B ⊥ S A ⇒ C B ⊥ ( S A B )
Do đó S C ; S A B ^ = C S B ^ = α
⇒ S B = a tan α = 5 a 10 ⇒ S A = S B 2 - A B 2 = a 6 2
Ta có S O ; A B C D ^ = S O A ^ trong đó t a n S C A ^ = S A O A = a 6 2 a 2 2 = 3 .

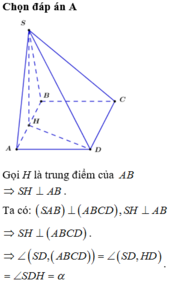
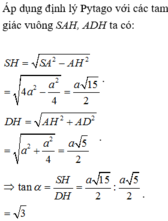
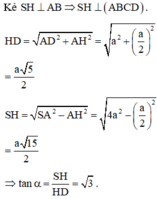
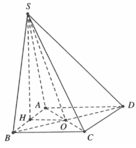




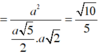

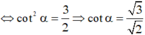

Vì S A ⊥ A B C D nên AC là hình chiếu vuông góc của SC lên (ABCD).
Góc giữa giữa SC và mp (ABCD) bằng góc SC&AC ⇒ α = SCA.
Xét tam giác SAC vuông tại A có
tan α = S A A C = a 6 a 2 = 3 ⇒ α = 60 o
Chọn D