làm giúp mình câu c ạ
K
Khách
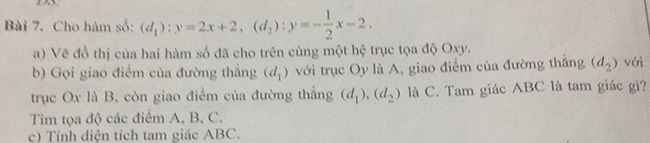
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
giúp mình câu c với ạ, 2 câu trên mình biết làm rồi
3
11 tháng 6 2023
c, \(2H_2+O_2 \rightarrow2H_2O\)
\(n_{H_2}=\dfrac{33,6}{22,4}=1,5(mol) \Rightarrow n_{O_2}=0,75(mol)\)
\(V_{O_2}=22,4.0,75=16,8(l)\)
H9
HT.Phong (9A5)
CTVHS
11 tháng 6 2023
\(n_{H_2}=\dfrac{33,6}{22,4}=1,5\left(mol\right)\)
a. PTHH: \(Fe+H_2SO_4\rightarrow FeSO_4+H_2\)
Theo PTHH: \(n_{Fe}=n_{H_2}=1,5\left(mol\right)\)
\(\Rightarrow m_{Fe}=56\cdot1,5=84\left(g\right)\)
b. Đổi: \(500ml=0,5l\)
\(CM_{H_2SO_4}=\dfrac{1,5}{0,5}=3M\)
c. \(2H_2+O_2\rightarrow2H_2O\)
Theo PTHH: \(n_{O_2}=\dfrac{1}{2}n_{H_2}=\dfrac{1}{2}\cdot1,5=0,75\left(mol\right)\)
\(\Rightarrow V_{O_2}=0,75\cdot22,4=16,8\left(l\right)\)
N
20 tháng 11 2021
\(a,C=\dfrac{81-1}{4\cdot9}=\dfrac{80}{36}=\dfrac{20}{9}\\ b,D=\dfrac{x+2\sqrt{x}+1+x-\sqrt{x}+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ D=\dfrac{2x+2\sqrt{x}+1}{x-1}\\ c,CD=\dfrac{x-1}{4\sqrt{x}}\cdot\dfrac{2x+2\sqrt{x}+1}{x-1}=\dfrac{2x+2\sqrt{x}+1}{4\sqrt{x}}=\dfrac{13}{8}\\ \Leftrightarrow52\sqrt{x}=16x+16\sqrt{x}+8\\ \Leftrightarrow16x-36\sqrt{x}+8=0\\ \Leftrightarrow4x-9\sqrt{x}+2=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=2\\\sqrt{x}=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\x=\dfrac{1}{16}\left(tm\right)\end{matrix}\right.\)
\(d,N=CD=\dfrac{2x+2\sqrt{x}+1}{4\sqrt{x}}=\dfrac{\sqrt{x}}{2}+\dfrac{1}{2}+\dfrac{1}{4\sqrt{x}}\\ \Leftrightarrow N\ge2\sqrt{\dfrac{\sqrt{x}}{2}\cdot\dfrac{1}{4\sqrt{x}}}+\dfrac{1}{2}=2\sqrt{\dfrac{1}{8}}+\dfrac{1}{2}=\dfrac{\sqrt{2}+1}{2}\)
Dấu \("="\Leftrightarrow4x=2\Leftrightarrow x=\dfrac{1}{2}\left(tm\right)\)
Vậy \(N_{min}=\dfrac{\sqrt{2}+1}{2}\)
MW
26 tháng 4 2023
CẤM KÉO CẦU THANG XUỐNG
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬TUI-NÓI-CẤM
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬Dừng lại! Đừng đi xuống.
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬ Bạn nghe tui! Đừng đi xuống đó
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬Bạn thật là đần độn khi cứ phớt lờ câu nói của tui như vậy đó....
╬═╬
╬═╬
╬═╬
╬═╬Nghiêm túc!!!TUI NÓI DỪNG LẠI!
╬═╬Cơ hội cuối cùng...đừng xuống đó
╬═╬
╬═╬
bây giờ bạn sẽ có 5 năm không may mắn, trừ khi bạn đăng câu này trên 5 web khác nhau~~
Đã bảo rồi mà ko nghe người ta cơ 🙂CẤM KÉO CẦU THANG XUỐNG
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬TUI-NÓI-CẤM
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬Dừng lại! Đừng đi xuống.
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬ Bạn nghe tui! Đừng đi xuống đó
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬Bạn thật là đần độn khi cứ phớt lờ câu nói của tui như vậy đó....
╬═╬
╬═╬
╬═╬
╬═╬Nghiêm túc!!!TUI NÓI DỪNG LẠI!
╬═╬Cơ hội cuối cùng...đừng xuống đó
╬═╬
╬═╬
bây giờ bạn sẽ có 5 năm không may mắn, trừ khi bạn đăng câu này trên 5 web khác nhau~~
Đã bảo rồi mà ko nghe người ta cơ 🙂
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 2 2021
Câu 4:
D và F cùng nhìn AC dưới 1 góc vuông nên tứ giác ACDF nội tiếp
\(\Rightarrow\widehat{ADF}=\widehat{ACF}\) (cùng chắn AF)
Tương tự, ABDE nội tiếp \(\Rightarrow\widehat{ABE}=\widehat{ADE}\) (cùng chắn AE)
Lại có \(\widehat{ABE}=\widehat{ACF}\) (cùng phụ góc \(\widehat{A}\))
\(\Rightarrow\widehat{ADE}=\widehat{ADF}\) hay AD là phân giác góc \(\widehat{FDE}\)
./
Hoàn toàn tương tự, ta cũng có CF là phân giác \(\widehat{DFE}\Rightarrow\widehat{BFD}=\widehat{AFE}\)
Mà \(\widehat{AFE}=\widehat{BFK}\Rightarrow\widehat{BFK}=\widehat{BFD}\)
\(\Rightarrow\dfrac{BK}{BD}=\dfrac{FK}{FD}\) theo định lý phân giác
Đồng thời \(\dfrac{CK}{CD}=\dfrac{FK}{FD}\) (CF là phân giác ngoài góc \(\widehat{DFK}\))
\(\Rightarrow\dfrac{BK}{BD}=\dfrac{CK}{CD}\Rightarrow\dfrac{BK}{CK}=\dfrac{BD}{CD}\)
Qua B kẻ đường thẳng song song AC cắt AK và AD tại P và Q
Theo Talet: \(\dfrac{BK}{CK}=\dfrac{BP}{AC}\) đồng thời \(\dfrac{BD}{DC}=\dfrac{BQ}{AC}\)
\(\Rightarrow\dfrac{BP}{AC}=\dfrac{BQ}{AC}\Rightarrow BP=BQ\)
Mặt khác BP song song MF (cùng song song AC)
\(\Rightarrow\dfrac{MF}{BP}=\dfrac{AF}{AB}\) ; \(\dfrac{NF}{BQ}=\dfrac{AF}{AB}\) (Talet)
\(\Rightarrow\dfrac{MF}{BP}=\dfrac{NF}{BQ}\Rightarrow MF=NF\)
A
1
10 tháng 12 2021
b: \(=\dfrac{2x-4-4x-8+8}{\left(x-2\right)\left(x+2\right)}=\dfrac{-2x-4}{\left(x-2\right)\left(x+2\right)}=\dfrac{-2}{x-2}\)
Bài 7:
a: Tọa độ điểm A là:
\(\left\{{}\begin{matrix}y=2\cdot0+2=2\\x=0\end{matrix}\right.\)