Giả sử F(x) là một họ nguyên hàm của hàm số f x = sin x x trên khoảng 0 ; + ∞ . Tính tích phân ∫ 1 3 sin 2 x x d x
A. F(3) - F(1)
B. F(6) - F(2)
C. F(4) - F(2)
D. F(6) - F(4)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

f ( x ) = 4 x - 1 ⇒ F ( x ) = ∫ f ( x ) d x = 2 x 2 - x + C
Phương trình hoành độ giao điểm của đồ thị hàm số F(x) và f(x) là:
2 x 2 - x + C = 4 x - 1 ⇔ 2 x 2 - 5 x + C + 1 = 0 ( * )
Do hai đồ thị hàm số trên cắt nhau tại một điểm trên trục tung nên x=0 là nghiệm của (*)
⇔ C + 1 = 0 ⇔ C = - 1
Với C=-1: Phương trình(*)
⇔ 2 x 2 - 5 x = 0 ⇔ [ x = 0 x = 5 2
Tọa độ các điểm chung của hai đồ thị hàm số trên là: (0;-1) và 5 2 ; 9
Chọn đáp án C.

Phương pháp:
+) Sử dụng các công thức nguyên hàm cơ bản
xác định hàm số F(x).
+) Giải phương trình hoành độ giao điểm.
Cách giải:
![]()
Phương trình hoành độ giao điểm của
đồ thị hàm số F(x) và f(x) là :
![]()
Do hai đồ thị hàm số trên cắt nhau tại một
điểm trên trục tung nên x=0 là nghiệm của (*)
![]()
![]()
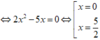
Tọa độ các điểm chung của hai đồ thị
hàm số trên là:
![]()
Đặt t = 2 nên dt = 2dx.
Đổi cận: x = 1 nên t = 2; x = 3 nên t = 6
F x = ∫ sin x x d x ⇒ F u = ∫ sin u u d u ∫ 1 3 sin 2 x x d x = ∫ 1 3 2 sin 2 x 2 x d x ⇒ ∫ 1 3 sin 2 x x d x = ∫ 2 6 sin u u d u = F 6 - F 2
Đáp án B