Người đi xe đạp khối lượng tổng cộng 60 kg) trên vòng xiếc bán kính 6,4 m phải đi qua điểm cao nhất với vận tốc tối thiểu bao nhiêu để không rơi.Cho g = 10 m / s 2
A. 15 m/s.
B. 8 m/s.
C. 12 m/s.
D. 9,3 m/s.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Tại điểm cao nhất của vòng xiếc có các lực tác dụng lên xe là trọng lực P → và phản lực Q → của vòng xiếc.
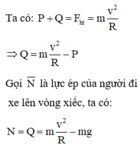
Muốn không bị rơi khỏi vòng xiếc, tức là vẫn còn lực ép lên vòng xiếc. Khi đó,
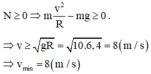

Chọn B.
Tại điểm cao nhất của vòng xiếc có các lực tác dụng lên xe là trọng lực P ⇀ và phản lực Q ⇀ của vòng xiếc.
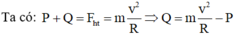
Gọi N→ là lực ép của người đi xe lên vòng xiếc, ta có:
N = Q = m v 2 /R - mg
Muốn không bị rơi khỏi vòng xiếc, tức là vẫn còn lực ép lên vòng xiếc.
Khi đó: N ≥ 0
→ m v 2 /R – mg ≥ 0
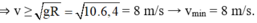

Chọn đáp án B
Tại điểm cao nhất của vòng xiếc có các lực tác dụng lên xe là trọng lực
![]() của vòng xiếc.
của vòng xiếc.
Ta có:
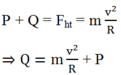
Gọi ![]() là lực ép của người đi xe lên vòng xiếc, ta có:
là lực ép của người đi xe lên vòng xiếc, ta có:
N = Q = mv2/R - mg
Muốn không bị rơi khỏi vòng xiếc, tức là vẫn còn lực ép lên vòng xiếc. Khi đó:
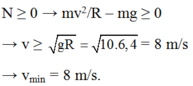

tại điểm cao nhất
Fht=P+N\(\Rightarrow N=F_{ht}-P\)
để người đi xe đạp đi qua điểm cao nhất mà ko rơi thì
N\(\ge\)0\(\Rightarrow\dfrac{v^2}{R}.m-m.g\ge0\)\(\Rightarrow\)vmin=8m/s2

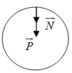
Ở điểm cao nhất người và xe đạp chịu tác dụng của các lực P → , N →
Theo định luật II Newton P → + N → = m a → Chiếu theo chiều hướng vào tâm
P + N = m a h t = m . v 2 R ⇒ N = m . v 2 R − P
Muốn không bị rơi thì người đó vẫn ép
lên vòng xiếc tức là
N ≥ 0 ⇒ m v 2 R − m g ≥ 0 ⇒ v ≥ g R
⇒ v min = g R = 8 m / s
Ở điểm cao nhất: P → + N → = m a →
⇒ N = m v 2 R − g = 65. 10 2 6 , 4 − 10 = 365 , 63 N
Lực nén: N ' = N = 365 , 63 N

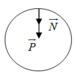
Người diễn viên chịu tác dụng của hai lực P → , N →
Theo định luật II Newton P → + N → = m a →
a. Chiếu theo chiều hướng vào tâm
P + N = m a h t = m . v 2 R ⇒ N = m . v 2 R − P
Muốn không bị rơi thì người đó vẫn ép lên vòng xiếc tức là
N ≥ 0 ⇒ m v 2 R − m g ≥ 0 ⇒ v ≥ g R ⇒ v ≥ 10.10 = 10 ( m / s )
Vậy vận tốc của xe đạp tối thiểu phải là 10m/s.
b. Chiếu theo chiều hướng vào tâm P cos α + N = m v 2 r
⇒ N = m v 2 r − g cos α = 60 10 2 10 − 10. cos 60 0 = 300 N

ở vị trí cao nhất
Fht=N+P\(\Rightarrow\)N=Fht-P=\(\dfrac{v^2}{R}.m-m.g\)
để người đó đi qua điểm cao nhất mà không rơi
N\(\ge\)0\(\Leftrightarrow\dfrac{v^2}{R}.m-m.g\ge0\Rightarrow v\ge8\)m/s
vmin=8m/s
lực nén lên vòng ở điểm cao nhất với v=10m/s
N=\(\dfrac{v^2}{R}.m-m.g\)=337,5N
Chọn B.
Tại điểm cao nhất của vòng xiếc có các lực tác dụng lên xe là trọng lực và phản lực của vòng xiếc.
Ta có:
Gọi N → là lực ép của người đi xe lên vòng xiếc, ta có:
N = Q = mv2/R - mg
Muốn không bị rơi khỏi vòng xiếc, tức là vẫn còn lực ép lên vòng xiếc.
Khi đó: N ≥ 0 → mv2/R – mg ≥ 0