Lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình vuông cạnh a và đường chéo BD' của lăng trụ hợp với đáy ABCD một góc 30º. Thể tích của lăng trụ là:
A . a 3 6 3
B . a 3 6 8
C . a 3 3
D . 3 a 3 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có
C ' C ⊥ A B C D , B D ⊥ O C ⇒ B D ⊥ O C ' ⇒ C O C ' ^ = 45 o
∆ O C C ' vuông cân tại C ⇒ C C ' = O C = a 2 2
Vậy V = a 2 . a 2 2 = a 3 2 2
Đáp án D

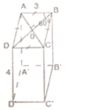
a) Sxq = 2.P.H (p: chu vi đáy; h: chiều cao)
= 3(3 + 3).4 = 48(cm2)
b) Gọi O là giao điểm của AC và BD. Vì tứ giác ABCD là hình thoi nên AC ⊥ BD tại O và có ∠ABC = 60o => ∠ABO = 30o
ΔABO là nửa tam giác đều nên
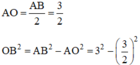
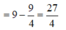
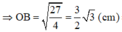
![]()
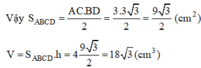

Đáp án A
Từ giả thiết ta có hình thang ABCD là hình thang nội tiếp được đường tròn nên nó là hình thang cân AB = AD = BC = a
Khi đó tâm đường tròn ngoại tiếp hình thang ABCD là trung điểm I của CD và bán kính là r = a.
Ta có:
![]()
=> A'A = a 3 . 3 = 3a => V = 3π a 3

Đáp án D
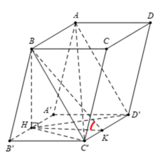
Gọi H là trung điểm của BC, kẻ H K ⊥ C ' D ' K ∈ C ' D '
Suy ra B H ⊥ A ' B ' C ' D ' ⇒ A C ' D ' ; A ' B ' C ' D ' ^ = B K H ^
Tam giác A’C’D’ đều cạnh 2 a ⇒ H K = d A ' ; C ' D ' = a 3
Tam giác BHK vuông tại H ⇒ B H = tan 60 ∘ x H K = 3 a
Diện tích hình thoi A’B’C’D’ là S A ' B ' C ' D ' = 2 a 2 3 .
Vậy thể tích khối lăng trụ ABC.A’B’C’D’ là V = B H . S A ' B ' C ' D ' = 3 a .2 a 2 3 = 6 3 a 3

Đáp án D
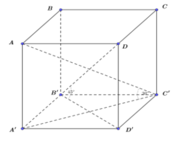
Ta dễ dàng tính được
![]()
Xét hình bình hành A’B’C’D’, ta dễ dàng tính được diện tích đáy S = 3 2 a 2
Suy ra thể tích khối lăng trụ đứng là:
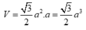
=> Chọn phương án D
Đáp án A