Một con lắc lò xo dao động điều hòa với phương trình: x = 4 cos ( ωt + π 6 ) ( cm ) . Sau thời gian ∆ t = 5 , 25 s (T là chu kì dao động) tính từ lúc t = 0, vật đi được quãng đường là:
A. 80,732m.
B. 81,462cm.
C. 85,464cm.
D. 96,836cm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Thế năng và động năng bằng nhau sau các khoảng thời gian Δt = 0,25T → T = 4Δt = 0,2 s
Độ cứng của lò xo 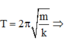
k = 50N/m

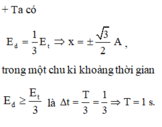
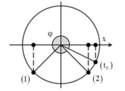
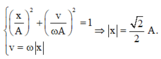
+ Tại t=0, vật đi qua vị trí x = 3 2 A , theo chiều dương. Biểu diễn các vị trí tương ứng trên đường tròn.
+ Trong một chu kì vật đi qua vị trí thỏa mãn yêu cầu bài toán 2 lần → tách 2016 = 2014+2
Vậy tổng thời gian là
![]()
Đáp án B

Đáp án B
+ Ta có
E d = 1 3 E t ⇒ x = ± 3 2 A
trong một chu kì khoảng thời gian E d ≥ E t 3 là Δ t = T 3 = 1 3 ⇒ T = 1 s .
+ Kết hợp với: x A 2 + v ω A 2 = 1 v = ω x ⇒ x = 2 2 A .
+ Tại t=0, vật đi qua vị trí x = 3 2 A theo chiều dương. Biểu diễn các vị trí tương ứng trên đường tròn
+ Trong một chu kì vật đi qua vị trí thỏa mãn yêu cầu bài toán 2 lần->2016=2014+2
Vậy tổng thời gian là Δ t = t φ + 1007 T = 23 24 + 1007 = 1007 , 958 s .

\(l_{max}=l_0+\Delta l+A\Rightarrow\left\{{}\begin{matrix}A=5cm=0,02m\\\Delta l=\dfrac{g}{\omega^2}=\dfrac{10}{\left(10\right)^2}=0,1m\\l_0=0,2m\end{matrix}\right.\)
=> \(l_{max}=0,2+0,1+0,02=0,32\left(m\right)=32cm\)
\(l_{min}=l_0+\Delta l-A=0,2+0,1-0,02=0,28\left(m\right)=28\left(cm\right)\)
Vậy ...
Đáp án C.
Phân tích ∆ t = 5 , 25 s = 5 T + T / 4
và trở về trạng thái ban đầu (trạng thái tại t = 0).
Xét tại t = 0 ta có
Như vậy sau 5T vật ở vị có x = 2 3 cm và đang chuyển động theo chiều âm của Ox.
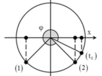
Để xác định quãng đường vật đi được trong thời gian T/4 tiếp theo ta có thể sử dụng vòng tròn lượng giác cho ly độ như hình vẽ bên.
Quãng đường S2 vật đi được trong thời gian T/4 này (tương ứng với chuyển động tròn đều từ M đến N) là: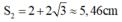
Vậy tổng quãng đường vật đã đi được là .
.