Cho hai đường thẳng phân biệt a; b và mặt phẳng
α
. Mệnh đề nào dưới đây đúng? ...
Đọc tiếp
Cho hai đường thẳng phân biệt a; b và mặt phẳng α . Mệnh đề nào dưới đây đúng?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
23 tháng 3 2017
Đúng(0)
Những câu hỏi liên quan
CM
12 tháng 11 2017
Các tam giác trên có hai loại:
+ Loại 1: Gồm các tam giác có 2 đỉnh điểm nằm trên a, 1 đỉnh nằm trên b. Số tam giác thuộc loại này là 
+ Loại 2: Gồm các tam giác có 1 đỉnh điểm nằm trên a, 2 đỉnh nằm trên b. Số tam giác thuộc loại này là 
Vậy theo quy tắc cộng, số tam giác cân tìm là: 120 + 168 = 288.
Chọn C.
LH
20 tháng 5 2017
Mỗi câu sau đây là đúng hay sai ?
a) Có một và chỉ một đường thẳng đi qua hai điểm (phân biệt) cho trước
Đúng
b) Có đúng ba đường thẳng đi qua ba điểm (phân biệt) cho trước
Sai
c) Có đúng 6 đường thẳng đi qua bốn điểm (phân biệt) cho trước
Sai
d) Hai đường thẳng phân biệt thì song song với nhau
Sai
e) Hai đường thẳng không cắt nhau thì song song với nhau
Sai
f) Hai đường thẳng không song song thì cắt nhau
Sai
g) Hai đường thẳng không phân biệt thì trùng nhau
Đúng
h) Ba đường thẳng phân biệt, từng đôi một cắt nhau thì có đúng 3 giao điểm (phân biệt)
Sai
CM
6 tháng 8 2017
Đáp án D
Dễ có số cách chọn 3 điểm từ 11 điểm đã cho là : C 11 3 = 165
Để 3 điểm được chọn tạo thành một tam giác thì phải thỏa mãn 3 điểm đó không thẳng hàng. Do đó có hai trường hợp xảy ra :
- Thứ nhất có hai điểm trên đường thẳng a và một điểm trên đường thẳng b
- Thứ hai có một điểm trên đường thẳng a và hai điểm trên đường thẳng b
Từ đây suy ra số cách chọn 3 điểm để tạo thành một tam giác là : C 6 2 C 5 1 + C 6 1 C 5 2 = 135
Vậy xác suất cần tìm là 135 165 = 9 11 . => Chọn đáp án D.
CM
5 tháng 10 2019
Đáp án D
Dễ có số cách chọn 3 điểm từ 11 điểm đã cho là : C 11 3 = 165
Để 3 điểm được chọn tạo thành một tam giác thì phải thỏa mãn 3 điểm đó không thẳng hàng. Do đó có hai trường hợp xảy ra :
- Thứ nhất có hai điểm trên đường thẳng a và một điểm trên đường thẳng b
- Thứ hai có một điểm trên đường thẳng a và hai điểm trên đường thẳng b
Từ đây suy ra số cách chọn 3 điểm để tạo thành một tam giác là : C 6 2 C 5 1 + C 6 1 C 5 2 = 135
18 tháng 9 2023
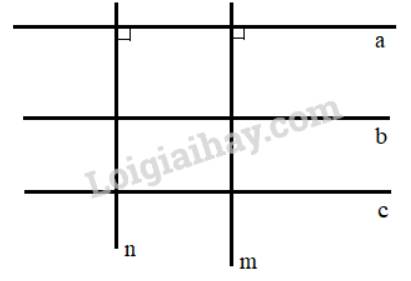
Ta có: +) a // b, b // c nên a // c ( Hai đường thẳng cùng song song với đường thẳng thứ ba thì chúng song song với nhau)
+) m \( \bot \) a; n \( \bot \)a nên m // n (Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)
Theo định lý “Đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì cũng vuông góc với đường thẳng kia, ta có:
+) a // b; a \( \bot \)n nên b \( \bot \)n
+) a // b; a \( \bot \)m nên b \( \bot \)m
+) a // c; a \( \bot \)n nên c \( \bot \)n
+) a // c; a \( \bot \)m nên c \( \bot \)m
Vậy các cặp đường thẳng song song là: a // b ; a // c ; b // c; m // n
Các cặp đường thẳng vuôn góc là: b \( \bot \)n; b \( \bot \)m; c \( \bot \)n; c \( \bot \)m; a \( \bot \)n; a \( \bot \)m
3 tháng 3 2016
Vậy cx nhảy vô trả lời. Tui L6 cx có thể lm mấy bài L5 trên mạng mà !!!
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
Cách 1:
TH1: 2 điểm thuộc a và 1 điểm thuộc b
Số cách chọn 2 điểm thuộc đường thẳng a là \(C_3^2\) (cách chọn)
Số cách chọn 1 điểm thuộc đường thẳng b là: \(C_4^1\) (cách chọn)
=> Số tam giác tạo thành là: \(C_3^2 . C_4^1 = 12\)
TH2: 2 điểm thuộc b và 1 điểm thuộc a
Số cách chọn 2 điểm thuộc đường thẳng b là \(C_4^2\) (cách chọn)
Số cách chọn 1 điểm thuộc đường thẳng a là: \(C_3^1\) (cách chọn)
=> Số tam giác tạo thành là: \(C_4^2 + C_3^1 = 18\)
Vậy có tất cả 12 + 18 = 30 tam giác.
Cách 2:
Số cách chọn 3 điểm thuộc đường thẳng a là: \(C_3^3\) (cách chọn)
Số cách chọn 3 điểm thuộc đường thẳng b là: \(C_4^3\) (cách chọn)
Số cách chọn 3 điểm bất kì trong 7 điểm đã cho là: \(C_7^3\) (cách chọn)
Số cách chọn 3 điểm không thẳng hàng trong 7 điểm đã cho là: \(C_7^3 - C_4^3 - C_3^3 = 30\) (cách chọn)
Vậy số tam giác có thể có là : 30 (tam giác)