Cho hình chóp S.ABC có SA
⊥
(ABC) tam giác ABC cân tại A, 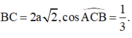Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC ...
Đọc tiếp
Cho hình chóp S.ABC có SA
⊥
(ABC) tam giác ABC cân tại A, 
Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC
K
Khách
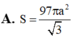
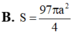
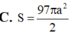
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
4 tháng 11 2019
Đúng(0)
Những câu hỏi liên quan
CM
27 tháng 10 2018
Đáp án B
Gọi H là trung diểm của BC suy ra cos A C B ^ = sin H A B ^ = 1 3 ⇒ cos H A B ^ = 2 2 3
Mà sin B A C ^ = 2 sin H A B ^ . cos H A B ^ = 4 2 9 nên theo định lí Sin, ta có R ∆ A B C = B C 2 s i n B A C ^ = 9 4
Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là R = R 2 ∆ A B C + S A 2 4 = a 97 4
Vậy diện tích mặt cầu cần tính là S = 4 πR 2 = 4 π a 97 4 2 = 97 πa 2 4
CM
2 tháng 5 2019
Chọn C.
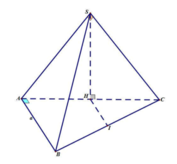
Gọi H, I lần lượt là trung điểm của BC, AC.
Tam giác SAC vuông cân tại S
Tam giác ABC vuông tại A => IA= IB = IC (1).
Lại có:
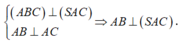
Mà HI là đường trung bình của tam giác ABC
Do đó: I là tâm mặt cầu ngoại tiếp hình chóp S.ABC
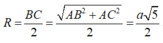
Vậy diện tích mặt cầu là
CM
9 tháng 2 2018
Đáp án D
Gọi H là trung điểm của BC ta có: A H ⊥ B C Do A B C ⊥ S B C ⇒ A H ⊥ S B C
Đặt A H = x ⇒ H C = a 2 − x 2 = H B = S H ⇒ Δ S B C
vuông tại S (do đường trùng tuyến bằng cạnh đối diện). Suy ra B C = S B 2 + S C 2 = a 3 . Gọi O là tâm đường tròn ngoại tiếp Δ A B C ⇒ O ∈ A H ⇒ O A = O B = O C = OS .Ta có: R = R A B C = A C 2 sin B , trong đó sin B = A H A B = A S 2 − S H 2 A B = 1 2 Do đó R C = a ⇒ S x q = 4 π R 2 C = 4 π a 2 .
CM
1 tháng 9 2017
Gọi O, I lần lượt là trung điểm của AC, SC.
Ta có:
∆ A B C vuông cân tại B ⇒ O là tâm đường tròn ngoại tiếp và A C = A B 2 = a 2 .
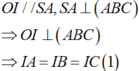
∆ S A C vuông tại A, I là trung điểm của S C ⇒ I S = I C = I A 2
Từ (1), (2) suy ra I là tâm mặt cầu ngoại tiếp hình chóp S.ABC, bán kính
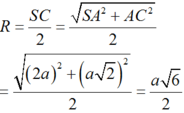
Chọn: A
