Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
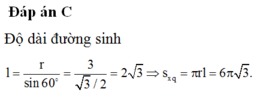
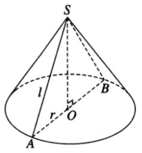
Theo giả thiết ta có góc ở đỉnh của hình nón là ∠ ASB = α = 120 ° . Gọi O là tâm của đường tròn đáy. Ta có: ∠ ASO = 60 °
và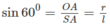 
với l là độ dài đường sinh của hình nón.
Vậy
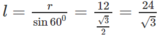
Khi có hai đường sinh vuông góc với nhau ta có tam giác vuông có diện tích là l 2 /2. Do đó, diện tích của thiết diện là:
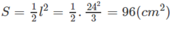
Đáp án B.
Đường kính đáy d = 2 R = 2 a 2 .
Do góc ở đỉnh bằng 60 0 nên thiết diện qua trục là tam giác đều.
Độ dài đường sinh là: l = d = 2 a 2
Diện tích xung quanh hình nón là:
S x q = π R l = π . a 2 .2 a 2 = 4 π a 2 .
a) Đường sinh l của hình nón là:
l = =
= 5√41 (cm).
Diện tích xung quanh của hình nón là:
Sxq = πrl = 125π√41 (cm2)
b) Vnón = = (625.20π)/3 = (12500π)/3 (cm3)
c) Giả sử thiết diện cắt hình tròn đáy theo đoạn thẳng AB.
GỌi I là trung điểm AB, O là đỉnh của nón thì thiết diện là tam giác cân OAB.
Hạ HK vuông góc AI, H là tâm của đáy, thì HK vuông góc ( OAB) và theo giả thiết HK = 12 (cm)
