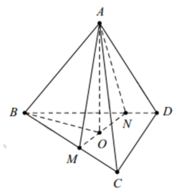
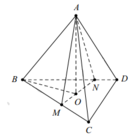
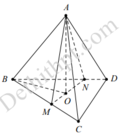
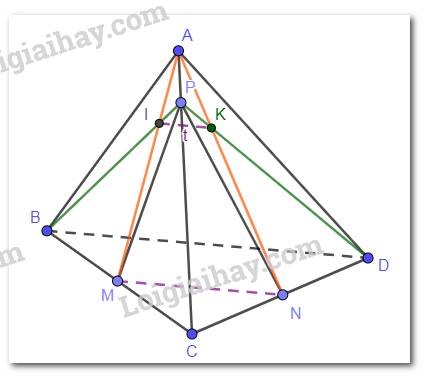
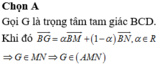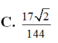Cho tứ diện ABCD, các điểm M,N thay đổi lần lượt trên các cạnh BC,BD sao cho B C B M + B D B N = 3 Mặt phẳng (AMN) luôn đi qua điểm cố định nào sau đây?
A. Trọng tâm của tam giác BCD
B. Tâm đường tròn ngoại tiếp tam giác BCD
C. Tâm đường tròn nội tiếp tam giác BCD
D. Trực tâm của tam giác BCD