

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a,+) Từ A vẽ AH _|_ (BCD) (theo giả thiết AB = AC = AD)
Nên \(\Delta ABH=\Delta ACH=\Delta ADH\)
=> HB = HC = HD
Vậy H là tâm đường tròn ngoại tiếp tam giác BCD
+) Ta có: \(AH=\sqrt{AB^2-BH^2}\) với \(BH=\dfrac{2}{3}BM=\dfrac{2}{3}\cdot\dfrac{a\sqrt{3}}{3}\)
\(\Rightarrow AH=\sqrt{a^2-\dfrac{3a^2}{9}}=\dfrac{a\sqrt{6}}{3}\)
b, Ta có: \(H=AH=\dfrac{a\sqrt{6}}{3};r=BH=\dfrac{a\sqrt{3}}{3}\)
Diện tích xung quanh hình trụ là:
\(S_{xq}=2\pi rh=2\pi.\dfrac{a\sqrt{3}}{3}.\dfrac{a\sqrt{6}}{3}=\dfrac{2\pi\pi^2\sqrt{2}}{3}\)
Thể tích khối trụ là:
\(V=\pi r^2h=\pi\left(\dfrac{a\sqrt{3}}{3}\right)^2.\dfrac{a\sqrt{6}}{3}=\dfrac{\pi a^3\sqrt{6}}{9}\)

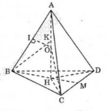
Từ A vẽ AH ⊥ (BCD)
Xét ba tam giác ABH, ACH và ADH có:
AB= AC = AD ( vì ABCD là tứ diện đều).
AH chung
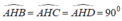
=> ∆ ABH = ∆ ACH =∆ ADH ( ch- cgv)
Suy ra,HB = HC = HD . Do đó, H là tâm đường tròn ngoại tiếp tam giác BCD
Do tam giác BCD là tam giác đều nên H đồng thời là trọng tâm tam giác BCD
Gọi M là trung điểm CD. Ta có;
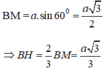
+ xét tam giác AHB vuông tại H có:
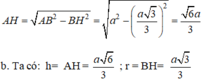

Chọn đáp án C
Ta có: MN là đường trung bình tam giác ACD.
=> CD // MN CD // (MNG)
Mặt khác: ![]()
Khi đó: Giao tuyến = ![]() = Gx // CD
= Gx // CD

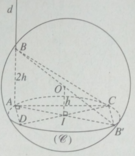
Diện tích tam giác BCD bằng:
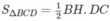
Diện tích này lớn nhất khi AI // CD.