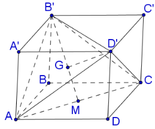
Biết rằng khối tứ diện đều cạnh bằng k thì có thể tích bằng 2 k 3 12 . Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a 2 . Tính theo a thể tích khối tứ diện A C B ' D ' .
A. 2 2 a 3 3
B. 2 a 3 6
C. 2 a 3 2
D. a 3 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thể tích 1 hình lập phương = cạnh x cạnh x cạnh = 3 x 3 x 3= 27(cm 3)
Thể tích 6 hình lập phương: 27 x 6= 162(cm3)
=>B

.png)
Gọi \(M\) là trung điểm của \(BC\), \(O\) là trọng tâm tam giác \(ABC\).
\( \Rightarrow SO \bot \left( {ABC} \right)\)
Tam giác \(ABC\) đều
\( \Rightarrow AM = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2} \Rightarrow AO = \frac{2}{3}AM = \frac{{a\sqrt 3 }}{3}\)
Tam giác \(SAO\) vuông tại \(O \Rightarrow SO = \sqrt {S{A^2} - A{O^2}} = \frac{{a\sqrt 6 }}{3}\)
\(\begin{array}{l}{S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}\\{V_{S.ABC}} = \frac{1}{3}{S_{\Delta ABC}}.SO = \frac{{{a^3}\sqrt 2 }}{{12}}\end{array}\)

Đáp án C
Nhận thấy chóp ACD′B′ có tất cả các
cạnh bằng nhau và bằng 2 2 a
Gọi M là trung điểm của AC, G là
trọng tâm của tam giác AB′C′.
Chóp ACD′B′ nhận D′G là đường cao.
Xét tam giác AB′C′ có


a: DM=AB/2=12cm
S ABMD=1/2(24+12)*24=12*36=432cm2
b: Xét ΔKMC và ΔKBA có
góc KMC=góc KBA
góc MKC=góc BKA
=>ΔKMC đồng dạng với ΔKBA
=>KM/KB=KC/KA=MC/AB=1/2
=>KC/KA=1/2
=>S ABK=2*S CBK
=>S ABK=192cm2
=>S ADMK=432-192=240cm2

Đáp án D
S O ' O N = 1 2 OO'.ON= 1 2 . a . a 2 = a 2 4 ; M O ' = a 2 . V M O ' O N = 1 3 M O ' . S O ' O N = a 3 24 .
Chọn đáp án A.
Chú ý: Tứ diện đều chỉ là trường hợp đặc biệt của một số tứ diện hoặc một hình chóp tam giác. Chúng ta có các kết quả như sau:
1. Cho khối chóp tam giác đều có cạnh đáy bằng a và cạnh bên bằng b. Thể tích khối chóp tam giác đều bằng
2. Cho khối tứ diện ABCD có và các cạnh còn lại đều bằng a. Thể tích khối tứ diện ABCD là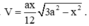
3. Cho khối tứ diện ABCD có AB = x, CD = y và các cạnh còn lại đều bằng a. Thể tích khối tứ diện ABCD là
4. Cho khối tứ diện gần đều ABCD có AB = CD = a, AC = BD = b, AD = BC = c. Thể tích khối tứ diện ABCD là