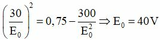Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án C.
Giả sử ở thời điểm t nào đó ta có như trên VTLG
Giả sử suất điện động xuất hiện trong khung dây có dạng e 1 = E 0 cos ω t 1 e 2 = E 0 cos ω t + 2 π 3 e 3 = E 0 cos ω t − 2 π 3 (1)
e 2 = E 0 cos ω t + 2 π 3 e 3 = E 0 cos ω t − 2 π 3 → e 2 - e 1 = ± 30 E 0 cos ω t + 2 π 3 − cos ω t − 2 π 3 = ± 30 ( 2 )
Áp dụng công thức toán học cos a − cos b = − 2 sin a + b 2 sin a − b 2
Phương trình (2) được viết lại: − 2 E 0 sin ω t sin 2 π 3 = ± 30 . Kết hợp với (1) ta có:
− 2 E 0 sin ω t sin 2 π 3 = ± 30 e 1 = E 0 cos ω t = 30 ⇔ E 0 sin ω t = ± 10 3 E 0 cos ω t = 30 ⇒ E 0 ± 10 3 2 + E 0 30 2 = 1 ⇒ E 0 = 20 3 ≈ 34 , 6 V
Chọn đáp án C
+ ta có: e 1 = E 0 cos ω t e 2 = E 0 cos ω t + 2 π 3 e 3 = E 0 cos ω t − 2 π 3 ⇒ e 2 − e 3 = E 0 cos ω t + 2 π 3 − cos ω t − 2 π 3
+ Lại có: cos ω t + 2 π 3 − cos ω t − 2 π 3 − 2 sin ω t . sin π 3 = − 3 sin ω t ⇒ e 2 − e 3 = E 0 3 sin ω t
+ Theo đề: e 1 = 30 ⇒ E 0 cos ω t = 30 e 2 − e 3 = 30 ⇒ E 0 3 sin ω t = 30 ⇒ 30 E 0 2 + 30 E 0 3 2 = cos 2 ω t + sin 2 ω t .
⇒ 30 E 0 2 + 30 E 0 3 2 = 1 ⇒ E 0 = 20 3 V ≈ 34 , 64 V
Đáp án B
+ Ta có: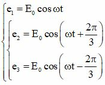 
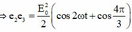
+ Theo đề 
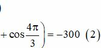
+ Biến đổi (2) ta co
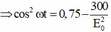(3)
+ Từ (1) và (3) ta có:
