- có ? số nguyên n thỏa mãn n2+2n-6/n-2 là số nguyên
- biết 22+22+23+24+22013 =2a vậy giá trị của a là ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
G
2
Những câu hỏi liên quan
26 tháng 2 2017
n2 + n3 - 13 chia hết cho n + 3
<=> n.(n+3) - 13 Chia hết cho n + 3
mà n.(n+3) chia hết cho n+3
=) 13 chia hết cho n+3
=) n+3 Thuộc Ư(13) = (-13 ;-1;1;13)
=) n thuộc (-16;-4;-;2;10 )
Vậy giá trị nhỏ nhất của N là - 16
26 tháng 2 2017
\(n^2+3n-13\) \(⋮n+3\)
\(\Leftrightarrow n\left(n+3\right)-13⋮n+3\)
Mà n(n+3) chia hết cho n+3
\(\Rightarrow\left(n+3\right)\inƯ\left(13\right)=\left(-13;-1;1;13\right)\)
\(\Rightarrow n\in\left(-16;-4;-2;10\right)\)
Vậy \(GTNN\)của \(n=-16\)
AH
Akai Haruma
Giáo viên
4 tháng 10
1/
Với $n$ nguyên để $\frac{n^2+2n-6}{n-2}$ là số nguyên thì:
$n^2+2n-6\vdots n-2$
$\Rightarrow n(n-2)+4(n-2)+2\vdots n-2$
$\Rightarrow 2\vdots n-2$
$\Rightarrow n-2\in \left\{\pm 1; \pm 2\right\}$
$\Rightarrow n\in \left\{3; 1; 4; 0\right\}$
AH
Akai Haruma
Giáo viên
4 tháng 10
Bạn xem lại đề câu 2. Với điều kiện đề cho thì không phù hợp với lớp 6 bạn nhé.
25 tháng 2 2023
\(P=\dfrac{n^3+3n^2+2n}{6}+\dfrac{2n+1}{1-2n}\)
Vì n^3+3n^2+2n=n(n+1)(n+2) là tích của 3 số liên tiếp
nên n^3+3n^2+2n chia hết cho 3!=6
=>Để P nguyên thì 2n+1/1-2n nguyên
=>2n+1 chia hết cho 1-2n
=>2n+1 chia hết cho 2n-1
=>2n-1+2 chia hết cho 2n-1
=>\(2n-1\in\left\{1;-1;2;-2\right\}\)
=>\(n\in\left\{1;0;\dfrac{3}{2};-\dfrac{1}{2}\right\}\)
BM
0
NK
1
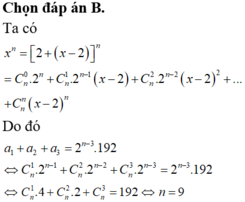
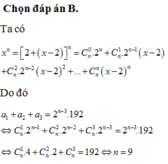
mìk chỉ biết câu 2 thui thông cảm nha
bn lấy các mẫu +lại cho nhau là đc rùi:
2+2+3+4+2013=2024
thầy ôn cho mik đó bn lm đi nha
Ở đây chia hết cho là chc nhé
Để n2+2n-6/n-2 là số nguyên thì n2+2n-6 chc n-2
=>(n2-22)+(2n-4)+2 chc n-2
=>(n+2)(n-2)+2(n-2)+2 chc n-2
mà (n+2)(n-2) chc n-2, 2(n-2) chc n-2
=>2 chc n-2
=>n-2 thuộc Ư(2)
=>n-2 thuộc {-1; 1; -2; 2}
=>n thuộc {1; 3; 0; 4}
Giải thích dòng 3, 4: mk áp dụng hằng đẳng thức(lên l7 học) a2-b2=(a+b)(a-b)