Hình tứ diện có bao nhiêu cạnh?
A. 5 cạnh
B. 3 cạnh
C. 4 cạnh
D. 6 cạnh
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 8 2023
Tổng diện tích hình vuông A,C,D :
\(5.5+2.2+3.3=40\left(cm^2\right)\)
mà tấm bìa cũng là hình vuông
Nên diện tích của hình vuông B là
\(49-40=9\left(cm^2\right)\)
Diện tích hình vuông A gấp \(\dfrac{25}{9}\) lần hình vuông B
CM
27 tháng 4 2018
Gọi (P) là mặt phẳng đi qua cạnh AB và song song với cạnh CD. Mặt phẳng (P) có vecto pháp tuyến n → vuông góc với hai vecto A B → = - 4 ; 5 ; - 1 v à C D → - 1 ; 0 ; 2
CM
21 tháng 2 2017
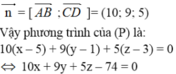
Đáp án C
Trong 5 cạch còn lại (không kể cạnh AB) chỉ có 3 cạnh AD, DB, AC khi quay quanh trục AB tạo ra các hình nón. Do đó có 3 hình nón được tạo thành (như hình vẽ).
Chú ý: Do CB ⊥ (ADB) => CB ⊥ AB, do đó CB quay quanh AB chỉ tạo ra hình tròn mà không phải là hình nón.
CM
29 tháng 3 2019
Đáp án C
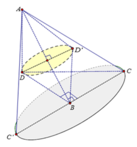
Trong 5 cạch còn lại (không kể cạnh AB) chỉ có 3 cạnh AD, DB, AC khi quay quanh trục AB tạo ra các hình nón. Do đó có 3 hình nón được tạo thành (như hình vẽ).
CM
24 tháng 5 2018
Đáp án là C
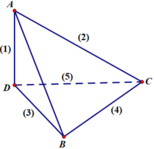
Điều kiện để tạo thành hình nón:
+ Cắt nhau ở đầu mút
+ Góc tạo bởi giữa 2 đường đó phải khác 90 độ
Áp vào hình ta sẽ được
+ AD thỏa mãn
+ AC thỏa mãn
+ DB thỏa mãn
+ BC không thỏa mãn vì BC vuông góc với (ADB) => góc ABC là 90 độ
+ CD không thỏa mãn vì không cắt AB
Vậy có 3 đường thỏa mãn
Đáp án D
Phương pháp:
Sử dụng định nghĩa hình tứ diện.
Cách giải:
Hình tứ diện có 6 cạnh.