Trong [0;π],phương trình sin x = 1 – cos 2 x có tập nghiệm là:
A. π 2
B. π 2 ; 3 π 2
C. 0 ; π
D. 0 ; π 2 ; π
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
20 tháng 9 2019
Đúng(0)
Những câu hỏi liên quan
16 tháng 11 2018
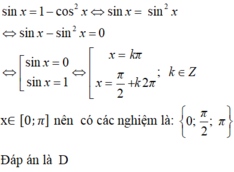
A đúng.
Mn là đơn chất nên có số oxi hóa 0
Fe3+ có số oxi hóa +3
SO3: x + 3.(-2) = 0 ⇒ x = 6 ⇒ số oxi hóa của S là +6
PO43-: x + 4.(-2) = -3 ⇒ x = 5 ⇒ số oxi hóa của P là +5
VT
21 tháng 4 2017
- Chọn C.
- Vì vật nhận nhiệt thì Q > 0, vật sinh công thì A < 0.
CM
4 tháng 2 2017
a) Chữ số 0 trong số 30 522 cho biết chữ số hàng nghìn là 0.
b) Chữ số 0 trong 8074 cho biết chữ số hàng trăm là 0.
c) Chữ số 0 trong số 205 316 cho biết chữ số hàng chục nghìn là 0.
d) Chữ số 0 trong số 200 463 cho biết chữ số hàng chục nghìn là 0 và chữ số hàng nghìn là 0.
9 tháng 10 2021
a. dòng sông, cửa sông, khúc sông, nước sông, sông cái .
- Sông Hồng là một con sông cái
b.cơn mưa, trận mưa, nước mưa, mưa rào, mưa xuân
Trời đang nắng bỗng nhiên một cơn mưa xuất hiện.
19 tháng 5 2021
Tóm tắt:
5 phút : 350 m
8 phút : ... m?
Bài giải:
1 phút người đó đi được số mét là:
350 : 5 = 70 (m)
8 phút người đó đi được số mét là:
70 x 8 = 560 (m)
Đ/S : 560 m
Chắc thế đó! Chúc một ngày tốt lành!
23 tháng 5 2022
Chứng minh rằng trực tâm H của tam giác ABC, trọng tâm G của tam giác A’B’C’ cùng nằm trên một đường thẳng đi qua O. Viết phương trình đường thẳng đó.
DD
Đoàn Đức Hà
Giáo viên
24 tháng 5 2022
Tọa độ điểm \(G\) là \(G\left(\dfrac{6+0+0}{3},\dfrac{0+4+0}{3},\dfrac{0+0+3}{3}\right)\) suy ra \(G\left(2,\dfrac{4}{3},1\right)\).
\(\overrightarrow{AB}=\left(-2,3,0\right),\overrightarrow{BC}=\left(0,-3,4\right),\overrightarrow{CA}=\left(2,0,-4\right)\)
Đặt \(H\left(a,b,c\right)\).
Vì \(H\) là trực tâm tam giác \(ABC\) nên
\(\left\{{}\begin{matrix}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{BH}.\overrightarrow{CA}=0\\\left[\overrightarrow{AB},\overrightarrow{AC}\right].\overrightarrow{AH}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3b+4c=0\\2a-4c=0\\12\left(a-2\right)+8b+6c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{72}{61}\\b=\dfrac{48}{61}\\c=\dfrac{36}{61}\end{matrix}\right.\) suy ra \(H\left(\dfrac{72}{61},\dfrac{48}{61},\dfrac{36}{61}\right)\).
\(\overrightarrow{OG}=\left(2,\dfrac{4}{3},1\right)\)
Đường thẳng qua OG: \(\left\{{}\begin{matrix}x=2t\\y=\dfrac{4}{3}t\\z=t\end{matrix}\right.\).
Bằng cách thử trực tiếp, ta thấy H nằm trên đường thẳng OG.
