cho 2 đoạn thẳng AB, CD cắt nhau tại trung điểm của mỗi đoạn. Gọi E,F theo thứ tự là trung điểm AD, BD. CM: CE, CF chia AB thành 3 phần bằng nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 5 2018
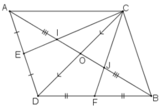
Gọi O là giao điểm của hai đoạn thẳng AB và CD.
⇒ AO = OB và CO = OD.
+ ΔACD có trung tuyến AO, CE cắt nhau tại I
⇒ I là trọng tâm ΔACD
⇒ AI = 2/3. AO = 2/3. 1/2. AB = 1/3.AB
+ Tương tự J là trọng tâm ΔBCD
⇒ BJ = 2/3. BO = 2/3. 1/2. BA = 1/3.AB
⇒ IJ = AB – AI – BJ = 1/3.AB
Vậy AI = IJ = JB
T
20 tháng 1 2016
Gọi K là giao điểm AB và CD
G là giao điểm CE và AB
I là giao điểm CF và AB
Vì K là trung điểm của AB => AK = KB = 1/2 AB
Xét tam giác ACD, có:
CE là đường trung tuyến ứng với AD (E là trung điểm AD)
AK là đường trung tuyến ứng với CD ( K là trung điểm CD)
=> G là trong tâm của tam giác ACD ( giao điểm 2 đường trung tuyến)
=> GK = 1/3 AK = 1/3 BK (*)
và AG = 2/3 AK = 1/3 AB (1)
Xét tam giác BCD, có:
CF là đường trung tuyến ứng với BD (F là trung điểm BD)
BK là đường trung tuyến ứng với CD (K là trung điểm CD)
=> I là trong tâm của tam giác BCD (giao điểm 2 đường trung tuyến)
=> IK = 1/3 BK (**)
và BI = 2/3 BK = 1/3 AB (2)
Từ (*) và (**) => IK + GK = 1/3 BK + 1/3 BK = 2/3 BK = 1/3 AB (3)
Từ 1 2 và 3 => AG = GI = IB = 1/3 AB
Vậy CE và CF chia AB làm 3 đoạn bằng nhau
18 tháng 5 2022
Gọi O là giao điểm của AB và CD
=>O là trung điểm chng của AB và CD
Xét ΔACD có
AO là đường trung tuyến
CE là đường trung tuyến
AO cắt CE tại I
Do đó: I là trọng tâm
=>AI=2/3AO=1/3AB(1)
Xét ΔCBD có
BO là đường trung tuyến
CF là đường trung tuyến
BO cắt CF tại J
Do đó; J là trọng tâm
=>BJ=2/3BO=1/3BA(2)
Từ (1) và (2) suy ra AI=BJ=1/3AB=JI
7 tháng 10 2022
a: Xét tứ giác ADBC có
I lad trung điểm chung của AB và CD
nên ADBC là hình bình hành
=>AD//BC và AD=BC
b: Xét tứ giác AMBN có
AM//BN
AM=BN
DO đó: AMBN là hình bình hành
Gọi giao của AN và BM với CD lần lượt là E và F
Xét ΔADE có
M là trung điểm của DA
MF//AE
DO đó: F là trung điểm của DE
=>DF=FE(1)
Xét ΔCFB có
N la trung điểm của CB
NE//FB
DO đó: E là trung điểm của CF
=>CE=EF(2)
Từ (1) và (2) suy ra CE=EF=FD
C
7 tháng 4 2022
\(E\) là trung điểm của \(AC\) nên \(AE=\)\(\dfrac{AC}{2}\)(1)
\(F\) là trung điểm của \(DB\) nên \(FB=\)\(\dfrac{DB}{2}\)(2)
từ (1) và (2) có:\(AE+FB=\)\(\dfrac{AC}{2}+\dfrac{DB}{2}\Rightarrow AE+FB=\dfrac{AC+BD}{2}\)
Trong đó :\(AE+FB=AB-EF\)
Vậy \(AE +FB=\)\(\dfrac{AC+BD}{2}=28-16=12\)
Suy ra:\(AC+BD=24\)
đoạn \(CD=AB-(AC+BD)=28-24=4cm\)