Cho hình phẳng (D) giới hạn bởi các đường y= x - 2 2 và y = 4. Tính thể tích của vật thể tròn xoay sinh ra bởi hình (D) khi nó quay xung quanh trục Ox
A. 118 π 5
B. 253 π 7
C. 112 π 3
D. 256 π 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
D quay xung quanh trục Oy
Ta có: y = ( x - 2 ) 2 ⇔ x - 2 = ± y ⇔ x = 2 ± y
V = π ∫ 0 4 2 + y 2 - 2 - y 2 dy = 8 π . ∫ 0 4 y dy = 8 π . 2 3 y 3 2 | 0 π = 128 π 3 đ v t t

Đáp án B.
Thể tích vật thể cần tính là:
V = π ∫ 1 a 1 x 2 d x = π ∫ 1 a d x x 2 = − π x a 1 = π − π a .

Phương pháp:
Thể tích vật thể được sinh ra khi
cho hình phẳng giới hạn bởi các đường
![]()
![]()
Cách giải:
Thể tích cần tìm là
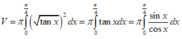
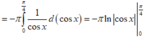
![]()
Chọn A.

Đáp án B
Ta có x = 0 ⇔ x = 0 x − 2 = 0 ⇔ x = 2 x = x − 2 ⇔ x = 4 x ≥ 0 .
Thể tích vật thể tròn xoay cần tính là: V = π ∫ 0 2 x 2 d x + π ∫ 2 4 x 2 − x − 2 2 d x = 16 π 3
D quay xung quanh trục Ox
Chọn D