Phương trình cos2x+4sinx+5=0 có bao nhiêu nghiệm trên khoảng
0
;
10
π
A. 2 B. 3 C. 4 D....
Đọc tiếp
Phương trình cos2x+4sinx+5=0 có bao nhiêu nghiệm trên khoảng 0 ; 10 π
A. 2
B. 3
C. 4
D. 5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 3 2019
Đáp án A
Dùng công thức
cos
2
x
=
1
-
2
sin
2
x
để đưa phương trình ban đầu về đa thức bậc 2 theo sin x.
Giải phương trình này tìm x và đối chiếu với yêu cầu
x
∈
0
;
10
π
để tìm được giá trị của x.
Ta có
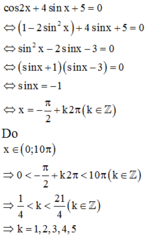
Do đó tập nghiệm của phương trình đã cho trên ( 0 ; 10 π ) là
CM
19 tháng 1 2019
Đáp án D
PT
⇔ 1 − 2 sin 2 x + 4 sin x + 5 = 0 ⇔ sin 2 x − 2 sin x − 3 = 0 ⇔ sin x = − 1 sin x = 3
⇒ sin x = − 1 ⇔ x = − π 2 + k 2 π k ∈ ℤ
Vì
x ∈ 0 ; 10 π ⇔ 0 < − π 2 + k 2 π < 10 π ⇔ 1 4 < k < 21 4 ⇒ k ∈ 1 ; 2 ; 3 ; 4 ; 5
NM
1
23 tháng 10 2021
\(cos2x+4sinx+5=0\Rightarrow1-2sin^2x+4sinx+5=0\)
\(\Rightarrow-2sin^2x+4sinx+6=0\) \(\Rightarrow\left[{}\begin{matrix}sinx=3\left(loại\right)\\sinx=-1\end{matrix}\right.\)
\(\Rightarrow sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)
Vậy pt có 1 họ nghiệm, và khi biểu diễn họ nghiệm trên 1 vòng tròn lượng giác ta được 1 nghiệm là \(x=-\dfrac{\pi}{2}+k2\pi\)
CM
9 tháng 9 2019
Đáp án C
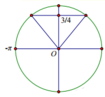
Phương trình đã cho ⇔ sin x = 3 4 ( 1 ) Quan sát đường tròn
lượng giác ta thấy có 2 giá trị của x ∈ - π ; π thỏa mãn phương trình (1).
Đáp án D