Cho tứ diện ABCD có tam giác ABC là tam giác cân với
B
A
C
=
120
0
,
A
B
=
A
C
=
a
.
Hình chiếu của D trên mặt phẳng ABC là trung điểm của BC. Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD biết thể tích của tứ diện ABCD là
V
=
a
3
16
.
A.
R
=
91
a
8
.
B.
R
=
a
13
...
Đọc tiếp
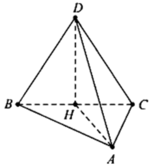
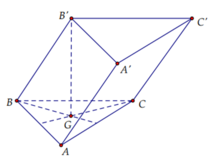
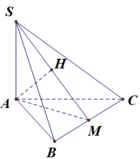
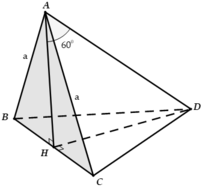
Cho tứ diện ABCD có tam giác ABC là tam giác cân với B A C = 120 0 , A B = A C = a . Hình chiếu của D trên mặt phẳng ABC là trung điểm của BC. Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD biết thể tích của tứ diện ABCD là V = a 3 16 .
A. R = 91 a 8 .
B. R = a 13 4 .
C. R = 13 a 2 .
D. R = 6 a .
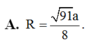
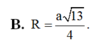
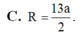
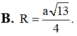
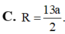
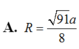
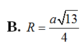
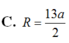
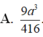
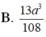
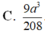
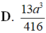
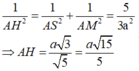
Đáp án A
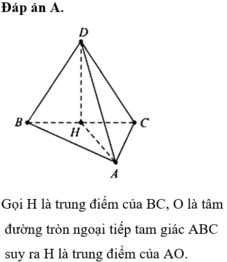
Gọi H là trung điểm của BC, O là tâm đường tròn ngoại tiếp tam giác ABC suy ra H là trung điểm của AO.
Ta có D H = 3. V A B C D S Δ A B C = a 3 4 .
Gọi J là tâm mặt cầu ngoại tiếp tứ diện ABCD.
Khi đó J O ⊥ A B C .
Do J A = R , O A = a nên J O = R 2 − a 2 .
Mặt khác H O ⊥ J O , H O ⊥ H D nên ta có
a 3 4 ± R 2 − a 2 2 + a 2 2 = R 2 ⇔ R = a 91 8 .