Cho biểu thức
M = log a a b - log a a b 4 + log a 3 b
Mệnh đề nào sau đây là đúng nhất?
A. 2 m = log m 16
B. 2 m = log 1 m 1 16
C. 2 m < log m 15
D. m = 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số \(y=log_cx\) nghịch biến
\(\Rightarrow0< c< 1\) và các hàm \(y=log_ax,y=log_bx\) đồng biến nên \(a,b>1\)
Ta chọn \(x=100\Rightarrow log_a>log_b100\Rightarrow a< b\Rightarrow b>a>c\)
\(\Rightarrow B\)

\(log_a\left(a^3b^2\right)=log_aa^3+log_ab^2=3+2\cdot log_ab\)
=>B

a: \(log_49=\dfrac{log9}{log4}=\dfrac{log3^2}{log2^2}=\dfrac{2\cdot log3}{2\cdot log2}=\dfrac{log3}{log2}=\dfrac{b}{a}\)
b: \(log_612=\dfrac{log12}{log6}=\dfrac{log2^2+log3}{log2+log3}=\dfrac{2\cdot log2+log3}{log2+log3}\)
\(=\dfrac{2a+b}{a+b}\)
c: \(log_56=\dfrac{log6}{log5}=\dfrac{log\left(2\cdot3\right)}{log\left(\dfrac{10}{2}\right)}=\dfrac{log2+log3}{log10-log2}\)
\(=\dfrac{a+b}{1-a}\)

\(a,A=log_23\cdot log_34\cdot log_45\cdot log_56\cdot log_67\cdot log_78\\ =log_28\\ =log_22^3\\ =3\\ b,B=log_22\cdot log_24...log_22^n\\ =log_22\cdot log_22^2...log_22^n\\ =1\cdot2\cdot...\cdot n\\ =n!\)

Vì \(\dfrac{1}{e}\simeq0,368< 1\)
\(\Rightarrow y=log_{\dfrac{1}{e}}\left(x\right)\) nghịch biến trên D = \(\left(0;+\infty\right)\)
Chọn C.
0<1/e<1
=>\(log_{\dfrac{1}{e}}\left(x\right)\) nghịch biến
=>C

\(P=loga^3+logb^2=log\left(a^3b^2\right)=log\left(100\right)=10\)

Đáp án D
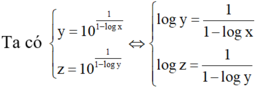
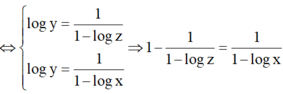
⇔ log z - 1 log z = 1 1 - log x
⇔ 1 - log x = log z log z - 1
⇔ log x = - 1 log z - 1 ⇔ x = 10 1 1 - log z .
Ta có
M = log a a b - 2 log a a b 4 + 3 log a b = log a a b - log a a b 2 + 3 = log a a b a 2 b + 3 = 2
Đáp án A