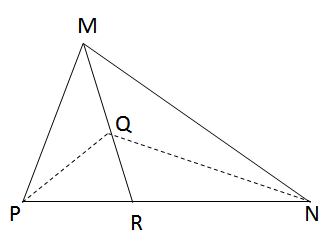
Cho tam giác MNP với trung tuyến MR và trọng tâm Q.
Tính tỉ số các diện tích của hai tam giác MPQ và RPQ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 5 2017
a) Vẽ PB ⊥ MR
Vậy tam giác MPQ và RPQ có chung đường cao PB
Vì Q là trọng tâm của ΔMNR nên MQ = 2QR
Ta có :
\(S\Delta MPQ=\frac{1}{2}MQ.PB=\frac{1}{2}.2QR.PB=QR.PB\)
\(S\Delta RPQ=\frac{1}{2}QR.PB\)
Vậy \(\frac{S\Delta MPQ}{S\Delta RPQ}=\frac{QR.PB}{\frac{1}{2}QR.PB}=2\)
b) Vẽ NA ⊥ MR
Vậy NA là đường cao của ΔMNQ đồng thời là đường cao của ΔRNQ.
Vì Q là trọng tâm của ΔMNP nên MQ = 2QR
Ta có :
\(S\Delta MNQ=\frac{1}{2}MQ.NA=\frac{1}{2}.2QR.NA=QR.NA\)
\(S\Delta RNQ=\frac{1}{2}QR.NA\)
Vậy \(\frac{S\Delta MNQ}{S\Delta RNQ}=\frac{QR.NA}{\frac{1}{2}QR.NA}=2\)
c) \(\Delta NRA=\Delta PRB\) => NA=PB
Ta có :\(S\Delta RPQ=\frac{1}{2}QR.PB=\frac{1}{2}QR.NA=S\Delta RNQ\)
Vậy SΔRPQ = SΔRNQ
- Từ kết quả câu a) ta có:
SΔQPM = 2SΔPRQ = SΔQNP (do câu c) (*)
- Từ kết quả câu b) ta có:
SΔQMN = 2SΔRNQ = SΔQNP (**)
Từ (*) và (**) suy ra:
SΔQMN = SΔQNP = SΔQPM (đpcm)
19 tháng 4 2017
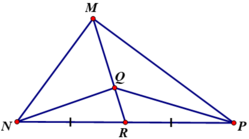
a) Vì Q là trọng tâm của ∆MNP nên điểm Q thuộc đường trung tuyến MR và MQRQ=2MQRQ=2.
Vì hai tam giác ∆MPQ và ∆RPQ có chung đường cao kẻ từ P nên :
SΔMPQSΔRPQ=MQRQ=2SΔMPQSΔRPQ=MQRQ=2 (1)
b) Chứng minh tương tự như câu (a) ta có :
SΔMPQSΔRPQ=2(2)SΔMPQSΔRPQ=2(2)
c) Hai tam giác ∆PQR và ∆QNR có chung đường cao kẻ từ Q và PR = RN nên S∆PQR = S∆QNR
Vì S∆PQR + S∆QNR = S∆PQN
Nên S∆PQN = 2.S∆PQR = 2.S∆QNR (3)
Từ (1), (2), (3) => S∆QMN = S∆QNP = S∆QPM
CM
19 tháng 10 2018
Δ RPQ và Δ RNQ có cùng đường cao.
Gọi m là độ dài đường vuông góc kẻ từ Q đến NP.
24 tháng 4 2017
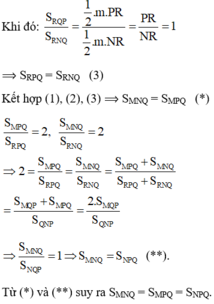
Hình tự vẽ nha =)
Ta có : S tam giác RNQ= đường cao hạ từ Q xuống MP nhân cho đáy RN
S tam giác RPQ=đường cao hạ từ Q xuống MP nhân cho đáy RP
Vì RN=RP ( MR là trung tuyến ứng với PN)
Vậy S tam giác RPQ=S tam giác RNQ
TT
19 tháng 5 2020
Cho hình thang vuông MNPQ có MN = 6dm , NP = 7dm , MQ =8dm ( như hình vẽ ) . Nối MP được hai hình tam giác MNP và MPQ .Tính tổng diện tích tam giác MNP và diện tích tam giác MPQ.
Δ MPQ và Δ RPQ có cùng đường cao.
Q là trọng tâm của ∆MNP ⟹ Q thuộc đường trung tuyến MR và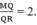
Gọi độ dài đường vuông góc kẻ từ P đến MR là h. Khi đó: