Xét tính liên tục của các hàm số sau trên tập xác định của chúng f ( x ) = x 2 - 2 x - 2 n ế u x ≠ 2 2 2 n ế u x = 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 7 2017
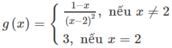
có tập xác định là D = R
- Nếu x ≠ 2 thì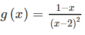 
là hàm phân thức hữu tỉ, nên nó liên tục trên các khoảng (-∞; 2) và (2; +∞)
Tại x = 2: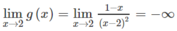 
Vậy hàm số y = g(x) không liên tục tại x = 2
Kết luận: y = g(x) liên tục trên các khoảng (-∞; 2) và (2; +∞) nhưng gián đoạn tại x = 2
CM
20 tháng 9 2018
Xét tính liên tục của hàm số sau trên tập xác định của nó:
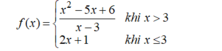
● Hàm số liên tục với mọi x ≠ 3.
● Tại x = 3, ta có:
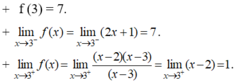
⇒ Hàm số không liên tục tại x = 3.
- Vậy hàm số liên tục trên các khoảng (-∞ ; 3), (3 ; +∞).
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
a) Hàm số \(f\left( x \right) = {x^2} + \sin x\) có tập xác định là \(\mathbb{R}\).
Hàm số x2 và sinx liên tục trên \(\mathbb{R}\) nên hàm số \(f\left( x \right) = {x^2} + \sin x\) liên tục trên \(\mathbb{R}\).
b) Hàm số \(g\left( x \right) = {x^4} - {x^2} + \frac{6}{{x - 1}}\) có tập xác định là \(\mathbb{R}\backslash \left\{ 1 \right\}.\)
Hàm số \({x^4} - {x^2}\) liên tục trên toàn bộ tập xác định
Hàm số \(\frac{6}{{x - 1}}\) liên tục trên các khoảng \(\left( {-\infty ;1} \right)\) và \(\left( {1; + \infty } \right).\)
Vậy hàm số đã cho liên tục trên các khoảng \(\left( {-\infty ;1} \right)\) và \(\left( {1; + \infty } \right).\)
c) Hàm số \(h\left( x \right) = \frac{{2x}}{{x - 3}} + \frac{{x - 1}}{{x + 4}}\) có tập xác định \(D = \mathbb{R}\backslash \left\{ {-4;3} \right\}.\)
Hàm số \(\frac{{2x}}{{x - 3}}\) liên tục trên các khoảng \(\left( {-\infty ;3} \right)\) và \(\left( {3; + \infty } \right).\)
Hàm \(\frac{{x - 1}}{{x + 4}}\) liên tục trên các khoảng \(\left( {-\infty ;-4} \right)\) và \(\left( {-4; + \infty } \right).\)
Vậy hàm số đã cho liên tục trên các khoảng \(\left( {-\infty ;-4} \right)\), \(\left( {-4;3} \right)\), \(\left( {3; + \infty } \right).\)
CM
22 tháng 7 2018
a) Đồ thị hàm số (hình bên).
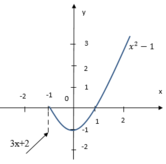
Quan sát đồ thị nhận thấy :
+ f(x) liên tục trên các khoảng (-∞ ; -1) và (-1 ; ∞).
+ f(x) không liên tục tại x = -1.
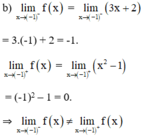
⇒ không tồn tại giới hạn của f(x) tại x = -1.
⇒ Hàm số không liên tục tại x = -1.
2
7 tháng 3 2023
`TXĐ: R`
`@` Nếu `x > 2` thì: `f(x)=2x+1`
H/s xác định trên `(2;+oo)`
`=>` H/s liên tục trên `(2;+oo)`
`@` Nếu `x < 2` thì: `f(x)=x^2-3x+4`
H/s xác định trên `(-oo;2)`
`=>` H/s liên tục trên `(-oo;2)`
`@` Nếu `x=2` thì: `f(x)=5`
`lim_{x->2^[-]} (x^2-3x+4)=2`
`lim_{x->2^[+]} (2x+1)=5`
Vì `lim_{x->2^[-]} f(x) ne lim_{x->2^[+]} f(x) =>\cancel{exists} lim_{x->2} f(x)`
`=>` H/s gián đoạn tại `x=2`
KL: H/s liên tục trên `(-oo;2)` và `(2;+oo)`
H/s gián đoạn tại `x=2`
14 tháng 7 2023
a: TXĐ: D=R
x^2;sin x đều liên tục trên R
=>f(x) liên tục trên R
b: TXĐ: D=R\{1}
x^4;-x^2;6/x-1 đều liên tục khi x thuộc (-vô cực;1) hoặc (1;+vô cực)
=>g(x) liên tục trên (-vô cực;1) và (1;+vô cực)
c: ĐKXĐ: x<>3; x<>-4
HS \(\dfrac{2x}{x-3}\) liên tục trên (-vô cực;3) và (3;+vô cực)
(x-1)/(x+4) liên tục trên (-vô cực;-4) và (-4;+vô cực)
=>h(x) liên tục trên từng khoảng xác định của nó
Tập xác định của hàm số là D = R
- Nếu x ≠ √2 thì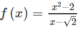
Đây là hàm phân thức hữu tỉ nên liên tục trên các khoảng (-∞; √2) và (√2; +∞)
- Tại x = √2:
Vậy hàm số liên tục tại x = √2
Kết luận : y = f(x) liên tục trên R