Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}x^2+3x+1=1+3\cdot1+1=5\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}2x+2=2\cdot1+2=4\)
f(1)=1+3+1=5
=>\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=f\left(1\right)\ne\lim\limits_{x\rightarrow1^-}f\left(x\right)\)
=>Hàm số bị gián đoạn tại x=1

\(\lim\limits_{x\rightarrow2}f\left(x\right)=\lim\limits_{x\rightarrow2}\dfrac{2-\sqrt{2x^2-4}}{2-x}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{4-2x^2+4}{2+\sqrt{2x^2-4}}\cdot\dfrac{1}{2-x}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{-2\left(x^2-4\right)}{-\left(x-2\right)\left(2+\sqrt{2x^2-4}\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{2\left(x-2\right)\left(x+2\right)}{\left(x-2\right)\left(2+\sqrt{2x^2-4}\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{2\left(x+2\right)}{2+\sqrt{2x^2-4}}=\dfrac{2\left(2+2\right)}{2+\sqrt{2\cdot2^2-4}}\)
\(=\dfrac{2\cdot4}{2+2}=\dfrac{8}{4}=2\)
\(f\left(2\right)=1\)
=>\(\lim\limits_{x\rightarrow2}f\left(x\right)< >f\left(2\right)\)
=>Hàm số bị gián đoạn tại x=2

\(\lim\limits_{x\rightarrow2}f\left(x\right)=\lim\limits_{x\rightarrow2}\dfrac{2x^2-7x+6}{2-x}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{2x^2-4x-3x+6}{-\left(x-2\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(3-2x\right)}{x-2}=\lim\limits_{x\rightarrow2}3-2x=3-2\cdot2=3-4=-1\)
\(f\left(2\right)=2\cdot2-5=-1\)
=>\(\lim\limits_{x\rightarrow2}f\left(x\right)=f\left(2\right)\)
=>Hàm số liên tục tại x=2

\(\lim\limits_{x\rightarrow2}f\left(x\right)=\lim\limits_{x\rightarrow2}\dfrac{x^2+x-6}{x-2}=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(x+3\right)}{x-2}=\lim\limits_{x\rightarrow2}\left(x+3\right)=5\\ f\left(2\right)=5\\ \rightarrow\lim\limits_{x\rightarrow2}f\left(x\right)=f\left(2\right)\)
Suy ra f(x) liên tục tại x = 2.

\(\lim\limits_{x\rightarrow5}f\left(x\right)=\lim\limits_{x\rightarrow5}\dfrac{x^2-8x+15}{x-5}\)
\(=\lim\limits_{x\rightarrow5}\dfrac{\left(x-3\right)\left(x-5\right)}{x-5}=\lim\limits_{x\rightarrow5}x-3=5-3=2\)
f(5)=2*5-1=9
=>\(f\left(5\right)\ne\lim\limits_{x\rightarrow5}f\left(x\right)\)
=>Hàm số gián đoạn tại x=5

\(\lim\limits_{x\rightarrow1}f\left(x\right)=\lim\limits_{x\rightarrow1}\dfrac{2x^2-5x+3}{x-1}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(2x-3\right)}{x-1}=\lim\limits_{x\rightarrow1}2x-3=2\cdot1-3=-1\)
f(1)=4
=>\(\lim\limits_{x\rightarrow1}f\left(x\right)< >f\left(1\right)\)
=>Hàm số bị gián đoạn tại x=1

\(\lim\limits_{x\rightarrow2}f\left(x\right)=\lim\limits_{x\rightarrow2}\dfrac{x^2-4}{2-x}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(x+2\right)}{-\left(x-2\right)}=\lim\limits_{x\rightarrow2}-\left(x+2\right)\)
\(=-\left(2+2\right)=-4\)
\(f\left(2\right)=2-7=-5\)
=>\(\lim\limits_{x\rightarrow2}f\left(x\right)< >f\left(2\right)\)
=>Hàm số gián đoạn tại x=2
Khi \(x\ne\)2 thì \(f\left(x\right)=\dfrac{x^2-4}{2-x}\) hoàn toàn xác định nên hàm số liên tục trên các khoảng \(\left(-\infty;2\right);\left(2;+\infty\right)\)

\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}-x^2+3x-2=-2^2+3\cdot2-2=0\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}x+3=2+3=5\)
f(2)=2+3=5
=>\(\lim\limits_{x\rightarrow2^+}f\left(x\right)\ne\lim\limits_{x\rightarrow2^-}f\left(x\right)=f\left(2\right)\)
=>Hàm số gián đoạn tại x=2

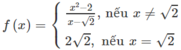
Tập xác định của hàm số là D = R
- Nếu x ≠ √2 thì 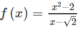
Đây là hàm phân thức hữu tỉ nên liên tục trên các khoảng (-∞; √2) và (√2; +∞)
- Tại x = √2:
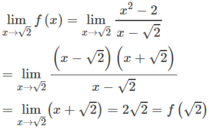
Vậy hàm số liên tục tại x = √2
Kết luận : y = f(x) liên tục trên R
`TXĐ: R`
`@` Nếu `x > 2` thì: `f(x)=2x+1`
H/s xác định trên `(2;+oo)`
`=>` H/s liên tục trên `(2;+oo)`
`@` Nếu `x < 2` thì: `f(x)=x^2-3x+4`
H/s xác định trên `(-oo;2)`
`=>` H/s liên tục trên `(-oo;2)`
`@` Nếu `x=2` thì: `f(x)=5`
`lim_{x->2^[-]} (x^2-3x+4)=2`
`lim_{x->2^[+]} (2x+1)=5`
Vì `lim_{x->2^[-]} f(x) ne lim_{x->2^[+]} f(x) =>\cancel{exists} lim_{x->2} f(x)`
`=>` H/s gián đoạn tại `x=2`
KL: H/s liên tục trên `(-oo;2)` và `(2;+oo)`
H/s gián đoạn tại `x=2`