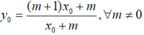Biết đồ thị (Cm) của hàm số y = (m+1)x + mx + m(m≢0) luôn đi qua một điểm M cố định khi m thay đổi. Tọa độ điểm M khi đó là
A. 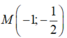
B. ![]()
C. ![]()
D. ![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, \(m=\dfrac{4}{3}\Leftrightarrow\left(d\right):y=-2:\dfrac{4}{3}\cdot x+2=-\dfrac{3}{2}+2\)
PT hoành độ giao điểm của (P) và (d) là
\(\dfrac{x^2}{2}=-\dfrac{3}{2}x+2\Leftrightarrow x^2=-3x+4\\ \Leftrightarrow x^2+3x-4=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=\dfrac{1}{2}\\y=8\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}A\left(1;\dfrac{1}{2}\right)\\B\left(-4;8\right)\end{matrix}\right.\)
Vậy \(A\left(1;\dfrac{1}{2}\right);B\left(-4;8\right)\) là tọa độ giao điểm của (P) và (d)
b, PT hoành độ giao điểm: \(\dfrac{x^2}{2}=-\dfrac{2}{m}x+2\Leftrightarrow x^2m=-4x+4m\)
\(\Leftrightarrow x^2m+4x-4m=0\left(1\right)\\ \Delta=16-4\left(-4m\right)m=16+8m^2>0,\forall m\)
Theo Vi-ét ta có \(x_1x_2=\dfrac{-4m}{m}=-4\) với \(x_1;x_2\) là nghiệm của (1)
Do đó \(x_1;x_2\) luôn trái dấu
Vậy PT(1) luôn có 2 nghiệm phân biệt trái dấu nên (P) luôn cắt (d) tại 2 điểm M,N nằm về 2 phía of trục tung
c, Gọi \(I\left(x_0;y_0\right)\) là điểm cố định mà (d) luôn đi qua
\(\Leftrightarrow y_0=-\dfrac{2}{m}\cdot x_0+2\Leftrightarrow my_0=-2x_0+2m\\ \Leftrightarrow m\left(y_0-2\right)+2x_0=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0=0\\y_0=2\end{matrix}\right.\Leftrightarrow I\left(0;2\right)\)
Điểm C,D là ở đâu bạn nhỉ?

Đáp án A
Với x = − 1 ta có y − 1 = − 4 . Vậy hàm số luôn đi qua điểm M − 1 ; − 4 ( có thể giải theo điểm cố định M x 0 ; y 0 )
Đáp án B
Gọi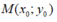 là điểm cố định cần tìm.
là điểm cố định cần tìm.
Ta có