Hỏi khi M thay đổi đồ thị
(
C
m
)
của hàm số y = 
- m - 1 đi qua bao nhiêu điểm cố định ?
A. 3
B.4
C.1
D.2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
-x + 3m đi qua bao nhiêu điểm cố định ?
CM
28 tháng 2 2018
Đáp án C
Gọi 
là điểm cố định cần tìm.
Ta có: 
.
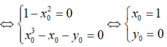
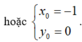Vậy đồ thị hàm số đã cho đi qua hai điểm cố định.
27 tháng 8 2021
c: Thay x=1 và y=-4 vào (d), ta được:
\(m-1+m+3=-4\)
\(\Leftrightarrow2m=-6\)
hay m=-3
là điểm cố định cần tìm.
- 2m +3 luôn đi qua một điểm M cố định khi m thay đổi, khi đó tọa độ của điểm M là
là điểm cố định cần tìm.
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
24 tháng 10 2023
a/
\(\Rightarrow3=4m.2-m-5\Leftrightarrow m=\dfrac{8}{5}\)
b/
Tọa độ A là \(A\left(x_0;y_0\right)\)
\(\Rightarrow y_0=4mx_0-m-5\forall m\)
\(\Leftrightarrow\left(4x_0-1\right)m-\left(y_0+5\right)=0\forall m\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x_0-1=0\\y_0+5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=\dfrac{1}{4}\\y_0=-5\end{matrix}\right.\)
=> d1 luân đi qua điểm A cố định \(A\left(\dfrac{1}{4};-5\right)\forall m\)
Tọa độ B là \(B\left(x_1;y_1\right)\)
\(\Rightarrow y_1=\left(3m^2+1\right)x_1+m^2-4\forall m\)
\(\Leftrightarrow3m^2x_1+x_1+m^2-4-y_1=0\forall m\)
\(\Leftrightarrow\left(3x_1+1\right)m^2+x_1-y_1-4=0\forall m\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x_1+1=0\\x_1-y_1-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{1}{3}\\y_1=-\dfrac{13}{3}\end{matrix}\right.\)
=> d2 luân đi qua điểm B cố định \(B\left(-\dfrac{1}{3};-\dfrac{13}{3}\right)\)
d/ d1//d2 khi
\(\left\{{}\begin{matrix}4m=3m^2+1\\-m-5\ne m^2-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m_1=1\\m_2=\dfrac{1}{3}\end{matrix}\right.\\m^2+m+1\ne0\end{matrix}\right.\)
Ta có \(m^2+m+1>0\forall m\)
\(\Rightarrow\left[{}\begin{matrix}m_1=1\\m_2=\dfrac{1}{3}\end{matrix}\right.\)
e/
\(\Rightarrow4mx-\left(m+5\right)=\left(3m^2+1\right)x+m^2-4\) tìm m để phương trình có nghiệm
Tìm giao
\(\Rightarrow4mx-\left(m+5\right)=\left(3m^2+1\right)x+m^2-4\) khi m=2
Thay m=2 tìm x rồi thay vào d1 hoặc d2 để tìm y
DD
Đoàn Đức Hà
Giáo viên
30 tháng 9 2021
Giả sử đồ thị hàm số đã cho luôn đi qua điểm cố định \(\left(x_0,y_0\right)\)với mọi \(m\).
\(y_0=\left(3m^2+1\right)x_0+m^2-4,\forall m\)
\(\Leftrightarrow m^2\left(3x_0+1\right)+x_0-y_0-4=0,\forall m\)
\(\Leftrightarrow\hept{\begin{cases}3x_0+1=0\\x_0-y_0-4=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x_0=-\frac{1}{3}\\y_0=-\frac{13}{3}\end{cases}}\)
Vậy điểm cố định mà đồ thị hàm số đã cho luôn đi qua có tọa độ là \(\left(-\frac{1}{3},-\frac{13}{3}\right)\).
Đáp án B
Gọi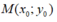
là điểm cố định cần tìm.
Ta có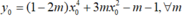
hoặc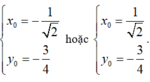
Vậy đồ thị hàm số đã cho đi qua bốn điểm cố định.