Vẽ giúp em cái hình ạ 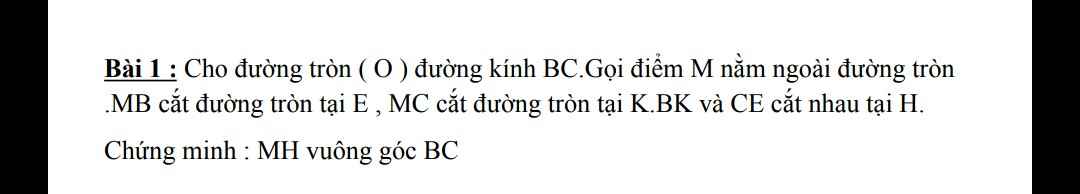
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: Xét ΔABD và ΔBAC có
BA chung
BD=AC
AD=BC
Do đó: ΔABD=ΔBAC
c: ta có: EA+EC=AC
EB+ED=BD
mà AC=BD
và EA=EB
nên EC=ED


A B C D M N
Xét tg ABC có
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}\left(gt\right)\) => MN//BC (Talet đảo trong tg)
Mà \(MN\in\left(DMN\right)\)
=> BC//(DMN)

Độ dài cạnh góc vuông lớn là:
\(\sqrt{6.4\cdot10}=8\left(cm\right)\)
Áp dụng HTL
\(AC^2=CH\cdot BC=6,4\left(6,4+3,6\right)=64\\ \Rightarrow AC=8\left(cm\right)\)
Vậy ...

a) Xét tứ giác MCNK có:
+ O là trung điểm của MN (gt).
+ O là trung điểm của CK (gt).
=> Tứ giác MCNK là hình bình hành (dhnb).
=> MC = KN và MC // KN (Tính chất hình bình hành).
b) Vì tứ giác MCNK là hình bình hành (cmt).
=> MK = CN và MK // CN (Tính chất hình bình hành).
c) Vì tứ giác MCNK là hình bình hành (cmt).
=> ^MCN = ^NKM (Tính chất hình bình hành).
d) Xét tứ giác ICHK có:
+ O là trung điểm của CK (gt).
+ O là trung điểm của IH (do OI = OH).
=> Tứ giác ICHK là hình bình hành (dhnb).
=> IK // CH (Tính chất hình bình hành).
Mà CH vuông góc MN (gt).
=> IK vuông góc MN (đpcm).

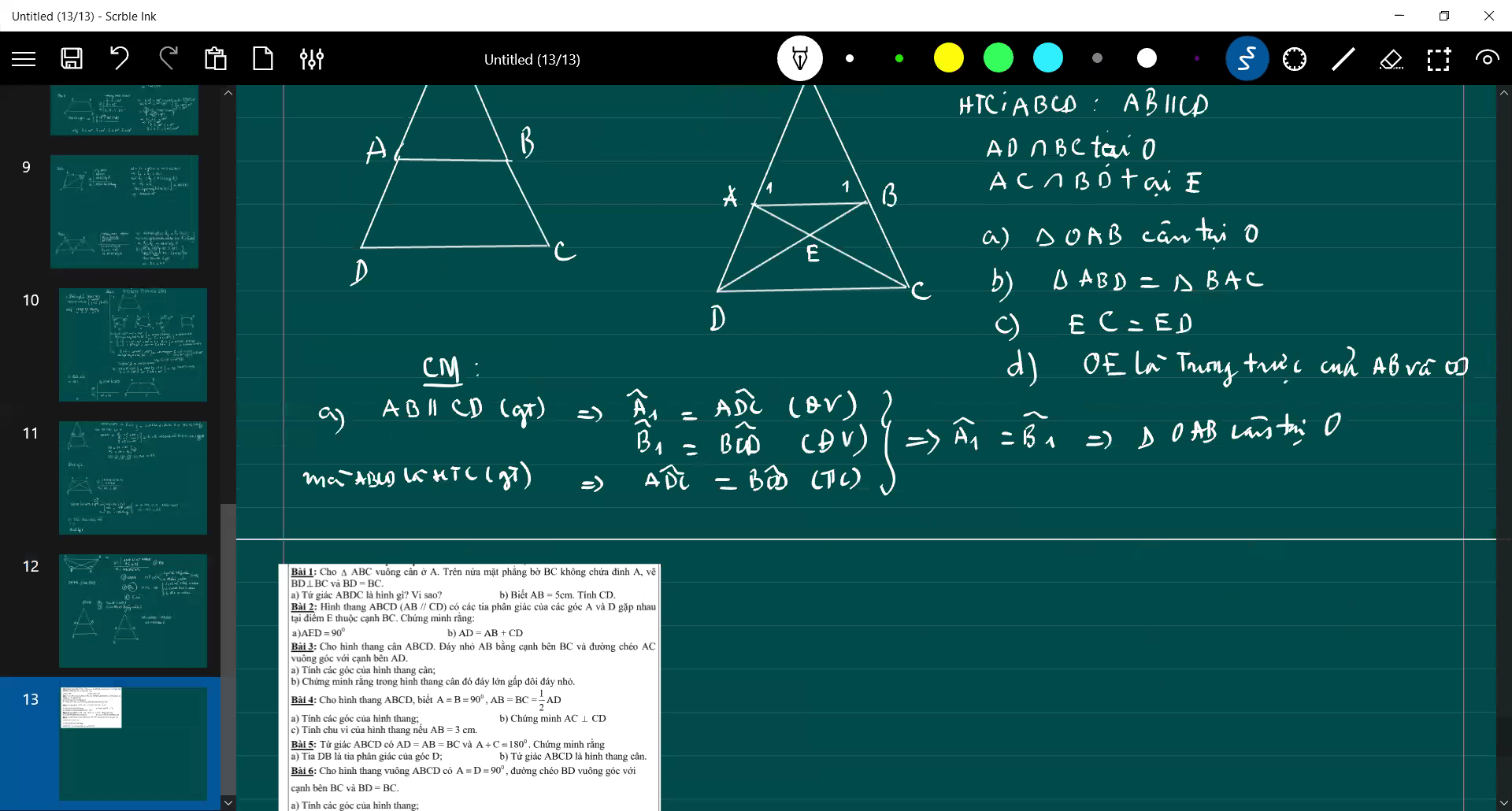

 vẽ giúp em cái sơ đồ dc kh ạ
vẽ giúp em cái sơ đồ dc kh ạ

Vì \(\widehat{BEC}=\widehat{BKC}=90^0\)(góc nt chắn nửa đg tròn) nên \(HK\perp MC;ME\perp HC\)
Xét tam giác HMC có 2 đường cao HK,ME (cm trên) cắt nhau tại B nên B là trực tâm
Do đó BC⊥MH