Trong số các số bên phải của các đa thức sau, số nào là nghiệm của đa thức bên trái nó?
M(x) = x 2 - 3 x + 2 ; - 2 - 1 1 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 9 2019
A(x) = 2x – 6
A(-3) = 2.(-3) – 6 = – 6 – 6 = –12 ≠ 0
A(0) = 2.0– 6 = 0 – 6 = – 6 ≠ 0
A(3) = 2.3 – 6 = 6 – 6 = 0
Vậy x = 3 là nghiệm của A(x).
CM
7 tháng 12 2019
Q(x) = x2 + x
Q(-1) = (-1)2 + (-1) = 1 – 1 = 0
Q(0) = 02 + 0 = 0 + 0 = 0
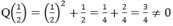
Q(1) = 12 + 1 = 1 + 1 = 2 ≠ 0.
Vậy -1 và 0 là nghiệm của Q(x).
CM
1 tháng 3 2018
P(x) = x2 + 5x – 6
P(-6) = (-6)2 + 5.(-6) – 6 = 36 – 30 – 6 = 0
P(-1) = (-1)2 + 5.(-1) – 6 = 1 - 5 – 6 = - 10 ≠ 0
P(1) = 12 + 5.1 – 6 = 1 + 5 – 6 = 0
P(6) = 62 + 5.6 – 6 = 36 + 30 – 6 = 60 ≠ 0
Vậy -6 và 1 là nghiệm của P(x).
7 tháng 5 2023
a. Thay x = 1 vào đa thức ta có:
\(1^2-4.1+4=1\)
Thay x = 2 vào đa thức ta có
\(2^2-4.2+4=0\)
Thay x = 3 vào đa thức ta có:
\(3^2-4.3+4=1\)
Thay x = -1 vào đa thức ta có:
\(\left(-1\right)^2-4.\left(-1\right)+4=9\)
b. Trong các số trên 2 là nghiệm của đa thức M(x)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
7 tháng 5 2023
a, M(\(x\)) = \(x^2\) - 4\(x\) + 4
M(1) = 12 - 4.1 + 4 = 1
M(2) = 22 - 4.2 + 4 = 0
M(3) = 32 - 4.3 + 4 = 1
M(-1) = (-1)2 - 4.(-1) + 4 = 9
b, Trong các số 1; 2; 3 và -1 thì 2 là nghiệm của M(\(x\)) vì M(2) = 0
21 tháng 5 2022
\(f\left(1\right)=1^4+2\cdot1^3-2\cdot1^2-6\cdot1+5\)
\(=1+2-2-6+5=0\)
=>x=1 là nghiệm
\(f\left(-1\right)=\left(-1\right)^4+2\cdot\left(-1\right)^3-2\cdot\left(-1\right)^2-6\cdot\left(-1\right)+5\)
\(=1-2-2+6+5=12-4=8\)
=>x=-1 không là nghiệm
\(f\left(2\right)=2^4+2\cdot2^3-2\cdot2^2-6\cdot2+5\)
\(=16+16-8-12+5=8+4+5>0\)
Do đó: x=2 không là nghiệm
\(f\left(-2\right)=\left(-2\right)^4+2\cdot\left(-2\right)^3-2\cdot\left(-2\right)^2-6\cdot\left(-2\right)+5\)
\(=16-16-2\cdot4+12+5=17-8=9>0\)
Do đó: x=-2 không là nghiệm
M(x) = x2 – 3x + 2
M(-2) = (-2)2 – 3.(-2) + 2 = 4 + 6 + 2 = 12 ≠ 0
M(-1) = (-1)2 – 3.(-1) + 2 = 1 + 3 + 2 = 6 ≠ 0
M(1) = 12 – 3.1 + 2 = 1 – 3 + 2 = 0
M(2) = 22 – 3.2 + 2 = 4 – 6 + 2 = 0
Vậy x = 1 và x = 2 là nghiệm của M(x).