Phương trình z 2 + 1 = 2 2 i có các nghiệm là z 1 , z 2 . Tính T = | z 1 | + | z 2 |
A. 2
B. 2 2
C. 2 3
D. 12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(z^2-4z+5=0\Rightarrow\left\{{}\begin{matrix}z_1+z_2=4\\z_1z_2=5\end{matrix}\right.\) theo hệ thức Viet
\(w=\dfrac{z_1+z_2}{z_1z_2}+i.z_1z_2\left(z_1+z_2\right)=\dfrac{4}{5}+i.5.4=\dfrac{4}{5}+20i\)

Chắc bạn ghi nhầm đề \(z_1\overline{z_2}+\overline{z_1}z_2\) mới có lý chứ nhỉ?
Khi pt bậc 2 có 2 nghiệm phức \(z_1;z_2\) thì \(z_1=\overline{z_2}\)
Do đó \(z_1\overline{z_2}+\overline{z_1}z_2=z_1^2+z_2^2=\left(z_1+z_2\right)^2-2z_1z_2=\left(-4\right)^2-2.7=2\)

Thay z = 1 + i vào phương trình đã cho ta có:
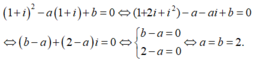
Chọn đáp án B.
Chọn C
Ta có: z 2 = - 1 + 2 2 i = 1 + 2 2 i + 2 i 2 = ( 1 + 2 i ) 2 <=> z 1 , 2 = ± ( 1 + 2 i )