Cho tam giác ABC cân tại A. Các điểm D, E theo thứ tự chuyển động trên cạnh AB, AC sao cho AD = AE. Trung điểm I của đoạn thẳng DE di chuyển trên đường nào?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 11 2017
Chứng minh được ADME là hình bình hành Þ I là trung điểm của AM. Tương tự 2A. I thuộc đường trung bình của D ABC (đường thẳng đi qua trung điểm của AB và AC)
TT
19 tháng 3 2016
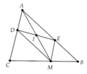
Ta nhận thấy rằng:
Nếu D trùng với B thì E trùng với A, đường trung trực của DE là đường trung trực của AB.
Nêu D trùng với A thì E trùng với C, đường trung trực của DE là đường trung trực của AC.
Do đó ta vẽ các đường trung trực của AB và cạnh AC, chúng cắt nhau tại O
Ta sẽ chứng tỏ rằng đường trung trực của DE đi qua O bằng cách chứng minh OD=OE
Gọi H và I theo thứ tự là trung điểm của AB và AC. Chứng minh HD=IE rồi suy ra tam giác OHD=tam giác OIE (cgc) để có OD=OE
Tương tự 2A.
Cho D º B, E º C Þ Vị trí điểm I.
CHo D º A, E º A Þ Vị trí điểm I.
Kết luận: I thuộc trung trực của BC.