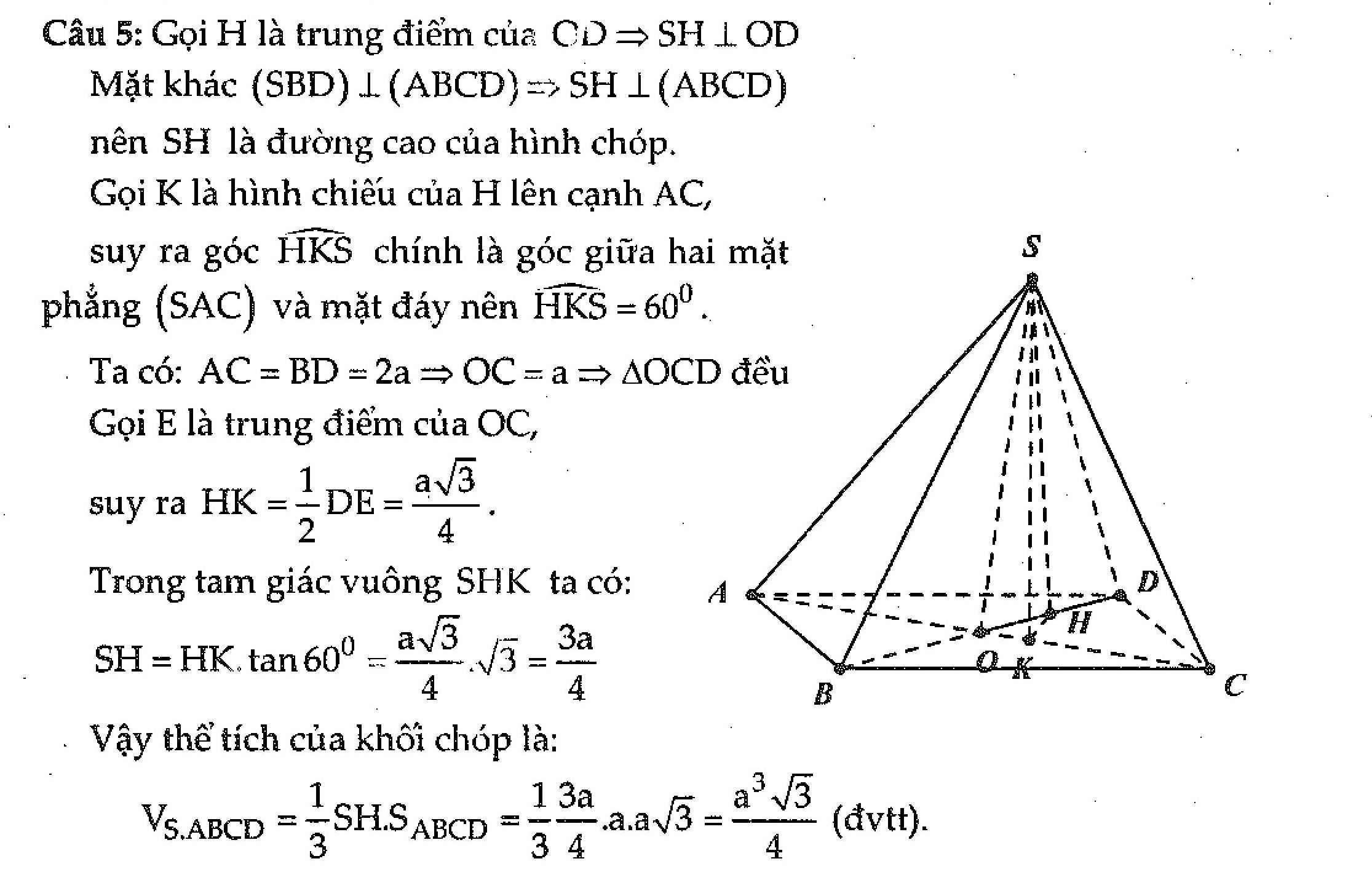
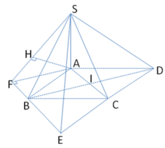
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, A D = a 6 , A B = a 3 ; M là trung điểm cạnh AD, hai mặt phẳng (SAC) và (SBM) cùng vuông góc với đáy; SA tạo với đáy góc 60 0 . Tính theo a thể tích khối chóp S.OMC.
A . a 3 6 8
A . 3 a 3 6 8
C . a 3 3 4
D . 3 a 3 3 4

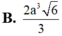
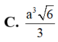
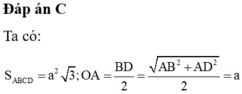
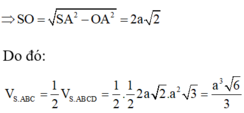
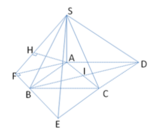

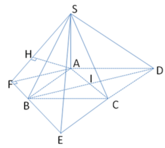
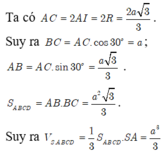
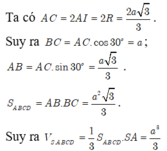

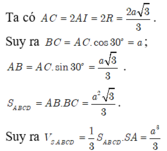

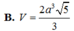
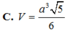
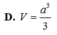
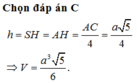
Đáp án A.
Gọi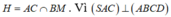 và (SBM)
⊥
(ABCD) nên SH
⊥
(ABCD)
và (SBM)
⊥
(ABCD) nên SH
⊥
(ABCD)
Có: AC =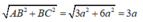
Vì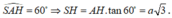
SH là đường cao của hình chóp S.OMC nên