Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình vuông cạnh a. Khoảng cách từ điểm A đến mặt phẳng (A’BCD’) bằng a 3 2 . Tính thể tích hình hộp theo a.

A. a 3
B. a 3 21 7
C. a 3 3
D. a 3 3 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
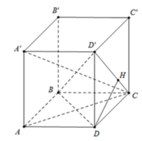
Tam giác A’AC vuông cân ⇒ A A ' = A C = A ' C 2 = a 2
Đáy ABCD là hình vuông nên A B = A D = A C 2 = a 2
Dựng D H ⊥ D ' C , lại có
B C ⊥ D C B C ⊥ D D ' ⇒ B C ⊥ D H S u y ra DH ⊥ B D ' C ⇒ d = D H = D C . D D ' C D 2 + D D ' 2 = a 6 6

Tam giác A'AC vuông cân tai A và A'C=a nên A'A=AC=\(\frac{a}{\sqrt{2}}\)
Do đó : \(AB=B'C'=\frac{a}{2}\)
\(V_{ABB'C}=\frac{1}{3}B'C'.S_{\Delta ABB'}=\frac{1}{6}B'C'.AB.BB'=\frac{a^3\sqrt{2}}{48}\)
Gọi H là chân đường cao kẻ từ A của tam giác A'AB. Ta có
\(\begin{cases}AH\perp A'B\\AB\perp BC\end{cases}\)\(\Rightarrow AH\perp\left(A'BC\right)\)
Nghĩa là \(AH\perp\left(BCD'\right)\Rightarrow AH=d\left(A,\left(BCD'\right)\right)\)
Ta có :
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AA'^2}\)
Do đó \(d\left(a,\left(BCD'\right)\right)=AH=\frac{a\sqrt{6}}{6}\)

Chọn đáp án B
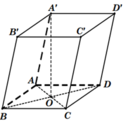
Gọi O = AC ∩ BD.Từ giả thiết suy ra A'O ⊥ ABCD
Cũng từ giả thiết, suy ra ABC là tam giác đều nên
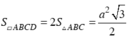
Đường cao khối hộp
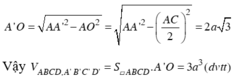
Đáp án C