Cho 6 điểm A, B, C, D, E, F. Khẳng định nào sau đây là đúng?
A. A B → + D C → = A C → + B D →
B. A B → + B C → = A C → + D B →
C. A D → + B E → + C F → = A E → + B F → + C D →
D. A B → = D C →
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đúng. Khi đó, ∆ABC = ∆FDE ( g.c.g)
b) Sai;
c) Đúng.
+)Vì ta có: ∠A + ∠B +∠C = 180º ( tổng ba góc của tam giác).
Và ∠D + ∠E + ∠F = 180º ( tổng ba góc của tam giác)
+) Lại có; ∠B = ∠D; ∠C = ∠E nên ∠A = ∠F
+) Kết hợp giả thiết suy ra: ∆ABC = ∆ FDE ( g.c.g)

Xét hai tam giác vuông ABC và DFE có: ∠A = ∠D = 90º ; AC=DE
a) Thêm điều kiện BC=EF thì ΔABC=ΔDFE (cạnh huyền - cạnh góc vuông).
b) Thêm điều kiện ∠C = ∠E thì ΔABC=ΔDFE (g.c.g).
c) Thêm điều kiện ∠C = ∠F thì ta không thể kết luận ΔABC=ΔDFE
a) Đúng;
b) Đúng;
c) Sai.

a) Đúng vì điểm C nằm trên d và hai điểm A, B không nằm trên d.
b) Sai vì ta kẻ được đường thẳng đi qua cả 3 điểm A, B, C.
c) Đúng vì điểm F không nằm trên m.
d) Đúng vì F không nằm trên đường thẳng DE.

Chọn B
Đáp án A sai do đường thẳng a có thể nằm trong mặt phẳng (EFG).
Đáp án C sai do mặt phẳng (ABC) có thể trùng với mặt phẳng (EFG).
Đáp án D sai do mặt phẳng (ABC) có thể trùng với mặt phẳng (EFG).

Nếu trong 4 điểm A, B, C, D không có ba điểm nào thẳng hàng thì ABCD tạo thành tứ giác.
Thêm điều kiện A B → = D C → chứng tỏ hai cạnh AB, CD song song và bằng nhau.
Vậy ABCD là hình bình hành.
Chọn D

Chọn A
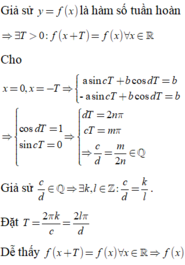
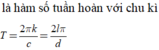
· Bổ trợ kiến thức: Thường thì ở những bài toán như trên các em có thể suy luận được ngay c d mới có sự liên quan và quyết định đến việc hàm số y = f(x)có tuần hoàn hay không.
Tuy nhiên chỉ cần nhận ra được chiều thuận “y= f(x)=asincx+bcosdx là hàm số tuần hoàn => c d là số hữu tỉ” là các em đã thấy ngay được phương án đúng rồi, để chứng minh chiều ngược lại thì đó là điều không dễ dàng.
Các em ghi nhớ luôn nhé – để áp dụng vào các bài tập khác: “Cho a,b,c,d là các số thực khác 0 và hàm số y= f(x)=asincx+bcosdx, khi đó y= f(x)=asincx+bcosdxlà hàm số tuần hoàn khi và chỉ khi c d là số hữu tỉ”
Đáp án C