Cho hai điểm A, B phân biệt và cố định, với I là trung điểm của AB. Tập hợp các điểm M thỏa mãn đẳng thức
2
M
A
→
+
M
B
→
=
M
A
→
+
2
M
B
→
là A. đường trung trực của đoạn thẳng AB B. đường tròn đường kính AB C. đường trung trực đoạn thẳng IA D. đường tròn tâm A; bán kính...
Đọc tiếp
Cho hai điểm A, B phân biệt và cố định, với I là trung điểm của AB. Tập hợp các điểm M thỏa mãn đẳng thức 2 M A → + M B → = M A → + 2 M B → là
A. đường trung trực của đoạn thẳng AB
B. đường tròn đường kính AB
C. đường trung trực đoạn thẳng IA
D. đường tròn tâm A; bán kính AB.
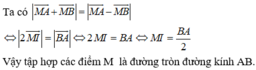
Chọn điểm E thuộc đoạn AB sao cho EB = 2EA ⇒ 2 E A → + E B → = 0 → .
Chọn điểm F thuộc đoạn AB sao cho FA = 2FB ⇒ 2 F B → + F A → = 0 → .
Ta có
2 M A → + M B → = M A → + 2 M B → ⇔ 2 M E → + 2 E A → + M E → + E B → = M F → + F A → + 2 M F → + 2 F B →
⇔ 3 M E → + 2 E A → + E B → ⏟ 0 → = 3 M F → + F A → + 2 F B → ⏟ 0 → ⇔ 3 M E → = 3 M F → ⇔ M E = M F . ( * )
Vì E ; F là hai điểm cố định nên từ đẳng thức (*) suy ra tập hợp các điểm M là trung trực của đoạn thẳng EF.
Gọi I là trung điểm của AB suy ra I cũng là trung điểm của EF
Vậy tập hợp các điểm M thỏa mãn 2 M A → + M B → = M A → + 2 M B → là đường trung trực của đoạn thẳng AB.
Chọn A.