Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
- Hàm số đã cho xác định với ∀x ∈ R.
- ta có:
- Phương trình tiếp tuyến tại điểm có hoành độ x = 1 là:
y = (m+ 6)(x – 1) + 3m + 1
- Tiếp tuyến này đi qua A(2; - 1) nên có:
- Vậy m = -2 là giá trị cần tìm.
\(y'=\dfrac{-3-m}{\left(x-1\right)^2}\) ; \(y\left(2\right)=m+5\) ; \(y'\left(2\right)=-m-3\)
Phương trình tiếp tuyến tại điểm có hoành độ \(x=2\):
\(y=\left(-m-3\right)\left(x-2\right)+m+5\)
\(\Leftrightarrow y=-\left(m+3\right)x+3m+11\)
Để tiếp tuyến cắt 2 trục tạo thành tam giác \(\Rightarrow m\ne\left\{-3;-\dfrac{11}{3}\right\}\)
Gọi A và B lần lượt là giao điểm của tiếp tuyến với Ox và Oy
\(\Rightarrow A\left(\dfrac{3m+11}{m+3};0\right)\) ; \(B\left(0;3m+11\right)\)
\(\Rightarrow OA=\left|\dfrac{3m+11}{m+3}\right|\) ; \(OB=\left|3m+11\right|\)
\(S_{OAB}=\dfrac{1}{2}OA.OB=\dfrac{25}{2}\Rightarrow\dfrac{\left(3m+11\right)^2}{\left|m+3\right|}=25\)
\(\Leftrightarrow\left(3m+11\right)^2=25\left|m+3\right|\Rightarrow\left[{}\begin{matrix}\left(3m+11\right)^2=-25\left(m+3\right)\\\left(3m+11\right)^2=25\left(m+3\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}9m^2+91m+196=0\\9m^2+41m+46=0\end{matrix}\right.\) \(\Rightarrow m=...\)
Pt hoành độ giao điểm của đồ thị hàm số (C) với đường thẳng d là:
\(\dfrac{x-1}{x+1}=m-x\Leftrightarrow\left\{{}\begin{matrix}x\ne-1\\g\left(x\right)=x^2+\left(2-m\right)x-m-1=0\left(1\right)\end{matrix}\right.\)
Đồ thị (C) cắt đường thẳng d tại 2 điểm phân biệt <=> pt(1) có 2 nghiệm phân biệt khác -1
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\g\left(-1\right)\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2+8>0\\-2\ne0\end{matrix}\right.\)
Khi đó: \(x_A,x_B\) là nghiệm của pt (1). Vì tiếp tuyến tại A và B //
\(\Rightarrow f'\left(x_A\right)=f'\left(x_B\right)\Leftrightarrow\dfrac{2}{\left(x_A+1\right)^2}=\dfrac{2}{\left(x_B+1\right)^2}\Leftrightarrow\left[{}\begin{matrix}x_A=x_B\left(loai\right)\\x_A+x_B=-2\end{matrix}\right.\)
Theo định lí Viet ta có:
\(x_A+x_B=m-2\Rightarrow m-2=-2\Leftrightarrow m=0\)
a:Sửa đề: y=x^3-3x^2+2
y'=3x^2-3*2x=3x^2-6x
y=2
=>x^3-3x^2=0
=>x=0 hoặc x=3
=>y'=0 hoặc y'=3*3^2-6*3=27-18=9
A(0;2); y'=0; y=2
Phương trình tiếp tuyến có dạng là;
y-2=0(x-0)
=>y=2
A(3;2); y'=9; y=2
Phương trình tiếp tuyến có dạng là:
y-2=9(x-3)
=>y=9x-27+2=9x-25
b: Tiếp tuyến tại M song song với y=6x+1
=>y'=6
=>3x^2-6x=6
=>x^2-2x=2
=>x=1+căn 3 hoặc x=1-căn 3
=>y=0 hoặc y=0
M(1+căn 3;0); y=0; y'=6
Phương trình tiếp tuyến là:
y-0=6(x-1-căn 3)=6x-6-6căn3
M(1-căn 3;0); y=0; y'=6
Phương trình tiếp tuyến là:
y-0=6(x-1+căn 3)
=>y=6x-6+6căn 3
+Ta có đạo hàm y’ = 3x2- 6mx+ 3( m+ 1) .
Do K thuộc ( C) và có hoành độ bằng -1, suy ra K( -1; -6m-3)
Khi đó tiếp tuyến tại K có phương trình
∆: y= ( 9m+ 6) x+ 3m+ 3
Đường thẳng ∆ song song với đường thẳng d
⇒ 3 x + y = 0 ⇔ y = - 3 x ⇔ 9 m + 6 = - 3 3 m + 3 ≠ 0 ⇔ m = - 1 m ≠ - 1
Vậy không tồn tại m thỏa mãn đầu bài.
Chọn D.
Đường tròn (S) tâm \(I\left(-1;-3\right)\) bán kính \(R=3\)
Thế tọa độ A vào pt (S) thỏa mãn nên A nằm trên đường tròn
Ta cần tìm B, C sao cho chi vi ABC lớn nhất
Đặt \(\left(AB;AC;BC\right)=\left(c;b;a\right)\Rightarrow\dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinC}=2R\)
\(\Rightarrow a+b+c=2R\left(sinA+sinB+sinC\right)\)
Mặt khác ta có BĐT quen thuộc \(sinA+sinB+sinC\le\dfrac{3\sqrt{3}}{2}\)
Dấu "=" xảy ra khi tam giác ABC đều
\(\Rightarrow a=b=c=2R.sin60^0=3\sqrt{3}\)
Khi đó I đồng thời là trọng tâm kiêm trực tâm \(\Rightarrow\left\{{}\begin{matrix}BC\perp AI\\d\left(A;BC\right)=\dfrac{a\sqrt{3}}{2}=\dfrac{9}{2}\end{matrix}\right.\)
\(\Rightarrow\) Phương trình BC có dạng \(y=-\dfrac{3}{2}\)
Hay (Cm) có 1 tiếp tuyến là \(y=-\dfrac{3}{2}\) (hệ số góc bằng 0 nên tiếp tuyến này đi qua 2 cực tiểu)
\(\Rightarrow m=-1\)
- Phương trình hoành độ giao điểm của d và (C) là
- Theo định lí Viet ta có x1+x2=-m; 
Giả sử A( x1; y1); B( x2; y2).
- Ta có 
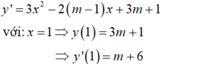
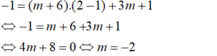
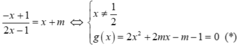
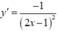nên tiếp tuyến của (C) tại A và B có hệ số góc lần lượt là 
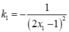và 
.Vậ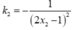y
- Dấu "=" xảy ra khi và chỉ khi m= -1.
Vậy k1+ k2 đạt giá trị lớn nhất bằng -2 khi m= -1.
Chọn A.
+ Phương trình hoành độ giao điểm của d và (C) là
+ Theo định lí Viet ta có x1+ x2= -m ; x1.x2= ( -m-1) /2.
Gọi A( x1; y1) ; B( x2: y 2) .
+ Ta có y ' = - 1 ( 2 x - 1 ) 2 , nên tiếp tuyến của ( C) tại A và B có hệ số góc lần lượt là
k 1 = - 1 ( 2 x 1 - 1 ) 2 ; k 2 = - 1 ( 2 x 2 - 1 ) 2
Dấu "=" xảy ra khi và chỉ khi m= -1.
Vậy k1+ k2 đạt giá trị lớn nhất bằng - 2 khi m= -1.
Chọn B.
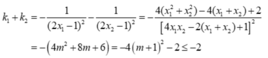
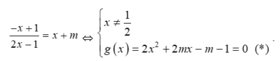
- Phương trình tiếp tuyến Δ của C m tại điểm có hoành độ x 0 = 2 là:
- Suy ra diện tích tam giác OAB là:
- Theo giả thiết bài toán ta suy ra:
Chọn A.