Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng tiếp xúc với (S): x 2 + y 2 + z 2 - 2 z - 4 y - 6 z - 2 = 0 và song song với (α): 4x + 3y - 12z+10 = 0
A. 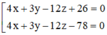
B. 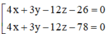
C. 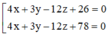
D. 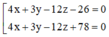
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Gọi I là tâm mặt cầu (S). Khi đó I (t; 1+t; 2+t) và ta có:
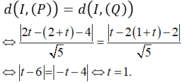
Vậy mặt cầu (S) có tâm I (1;2;3) và bán kính 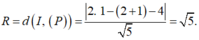
Do đó mặt cầu (S) có phương trình: ![]()

Đáp án B
Pt pháp tuyến của mặt phẳng cần tìm là n ⇀ = d , ⇀ ∆ ⇀ = (1;0;1)
Pt có dạng: x+z+D=0
Khoảng cách từ O (-1;1;-2) đến mp là 2
⇒ D=1
Pt có dạng : x+z+1=0

Ta có: (S) có tâm I 1 , 0 , - 2 và bán kính R = 6 .
d 1 có VTCP là: u 1 → 3 , - 1 , - 1
d 2 có VTCP là: u 2 → 1 , 1 , - 1
Ta có:
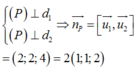
Khi đó ta có phương trình (P) có dạng:
x + y + 2 z + d = 0
Mặt phẳng (p) tiếp xúc với mặt cầu
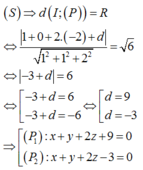
Chọn B.

Chọn D
Gọi vectơ pháp tuyến của mặt phẳng (P) là ![]() , a²+b²+c²>0.
, a²+b²+c²>0.
Phương trình mặt phẳng (P): a(x-4)+b (y-3)+c (z-4)=0.
Do (P) // Δ nên -3a+2b+2c=0 => 3a = 2 (b + c)
Mặt phẳng (P) tiếp xúc với (S) nên
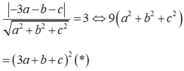
Thay 3a=2 (c+b ) vào (*) ta được:
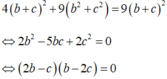
TH1: 2b-c=0, chọn b=1; c=2 => a = 2 => (P): 2x+y+2z-19=0 (thỏa).
TH2: b-2c=0, chọn c=1; b=2 => a = 2 => (P): 2x+2y+z-18=0 (loại do Δ ⊂ (P))

Đáp án là A.
+ Mặt phẳng chứa Ox có dạng B y + C z = 0
+ Do mặt cầu tiếp xúc với mặt phẳng nên:
2 B − C B 2 + C 2 = 1 ⇔ B = 0 B = 4 , C = 3
Vậy mặt phẳng cần tìm 4 y + 3 z = 0

Đáp án là A.
+ Mặt phẳng chứa Ox có dạng By+Cz=0
+ Do mặt cầu tiếp xúc với mặt phẳng nên 2 B - C B 2 + C 2 = 1 ⇔ B = 0 B = 4 , C = 3
Vậy mặt phẳng cần tìm 4y +3z=0

Chọn A
Mặt cầu (S) có tâm I (1; 2; -1) và bán kính R = 1
Gọi vectơ pháp tuyến của mặt phẳng (Q) là ![]() với
với
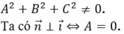
Mặt khác (Q) chứa trục hoành nên (Q) có phương trình dạng (Q): By + Cz = 0
Lại có (Q) tiếp xúc mặt cầu (S) nên
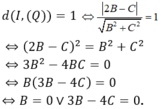
+ Với B = 0 thì phương trình mặt cầu là z = 0 ( chính là mặt phẳng 0xy)
+ Với 3B – 4C = 0, chọn B = 4 => C = 3. Vậy (Q): 4y + 3z = 0
Đáp án D
Phương pháp:
(P) // (α) => Phương trình mặt phẳng (P) có dạng 4x + 3y - 12z + D = 0 (D ≠ 0)
(P) tiếp xúc với (S) => d(I;(P)) = R với I; R là tâm và bán kính mặt cầu (S)
Cách giải:
Gọi mặt phẳng (P) là mặt phẳng cần tìm
(P) // (α) Phương trình mặt phẳng (P) có dạng 4x + 3y - 12z + D = 0 (D ≠ 0)
Mặt cầu (S) có tâm I (1;2;3), bán kính R = 4
(P) tiếp xúc với (S) => d(I;(P)) = R
Vậy mặt phẳng (P) thỏa mãn yêu cầu bài toán có phương trình