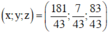Giải hệ phương trình x + 4 y - 2 z = 1 - 2 x + 3 y + z = - 6 3 x + 8 y - z = 12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Rõ ràng \(x=y=z=0\) là nghiệm của hệ
Với \(xyz\ne0\), Ta có
\(y=\frac{2x^2}{x^2+1}\le\frac{2x^2}{2x}=x\)
\(z=\frac{3y^3}{y^4+y^2+1}\le\frac{3y^3}{3y^2}=y\)
\(x=\frac{4z^4}{z^6+z^4+z^2+1}\le\frac{4z^4}{4z^3}=z\)
Suy ra \(y\le x\le z\le y\Rightarrow x=y=z\)
Từ pt thứ nhất của hệ suy ra
\(\frac{2x^2}{x^2+1}=x\Leftrightarrow2x=1=x^2\)( vì \(x\ne0\))\(\Leftrightarrow x=1\)
Vậy hệ pt có hai nghiệm \(\left(0,0,0\right)\)và \(\left(1,1,1\right)\)

Ta có x + y + z = 0
<=> (x + y + z)2 = 0
<=> \(x^2+y^2+z^2+2xy+2yz+2zx=0\)
\(\Leftrightarrow xy+yz+zx=-3\) (vì x2 + y2 + z2 = 6)
\(\Leftrightarrow x\left(y+z\right)+yz=-3\)
\(\Leftrightarrow-x^2+yz=-3\Leftrightarrow yz=x^2-3\) (vì x + y + z = 0)
Khi đó \(x^3+y^3+z^3=x^3+(y+z).(y^2+z^2-yz)\)
\(=x^3-x.[6-x^2-(x^2-3)]\)
\(=x^3-x.(9-2x^2)=3x^3-9x=6\)
Ta được \(\Leftrightarrow x^3-3x-2=0\Leftrightarrow(x^3+1)-3(x+1)=0\)
\(\Leftrightarrow(x+1)(x^2-x-2)=0\)
\(\Leftrightarrow\left(x+1\right)^2\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)
Với x = -1 ta có hệ \(\left\{{}\begin{matrix}y+z=1\\y^2+z^2=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1-z\\(1-z)^2+z^2=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1-z\\z^2-z-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1-z\\\left[{}\begin{matrix}z=-1\\z=2\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}y=2\\z=-1\end{matrix}\right.\\\left\{{}\begin{matrix}y=-1\\z=2\end{matrix}\right.\end{matrix}\right.\)
Với x = 2 ta có hệ : \(\left\{{}\begin{matrix}y+z=-2\\y^2+z^2=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-2-z\\(-2-z)^2+z^2=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-2-z\\z^2+2z+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-2-z\\z=-1\end{matrix}\right.\Leftrightarrow y=z=-1\)
Vậy (x;y;z) = (2;-1;-1) ; (-1 ; 2 ; -1) ; (-1 ; -1 ; 2)

x+y+z=1;x^2+y^2+z^2=1;x^3+y^3+z^3=1
=>x+y+z=x^2+y^2+z^2=x^3+y^3+z^3=1
=>x=y=z=1
x = y = z = 1
\(\Rightarrow\) x + y + z = 3
mà đề bảo x + y + z = 1
\(\Rightarrow\) làm sai

Làm hơi tắt , thông cảm ;))
Từ (1) \(\Rightarrow36=\left(x+y+z\right)^2\Leftrightarrow36=x^2+y^2+z^2+2\left(xy+yz+zx\right)\)
\(\Leftrightarrow36=18+2\left(xy+yz+zx\right)\Leftrightarrow xy+yz+zx=9\)(4)
Từ (3) \(\Rightarrow16=\left(\sqrt{x}+\sqrt{y}+\sqrt{z}\right)^2\Leftrightarrow16=x+y+z+2\left(\sqrt{xy}+\sqrt{yz}+\sqrt{zx}\right)\)
\(\Leftrightarrow\sqrt{xy}+\sqrt{yz}+\sqrt{zx}=5\Leftrightarrow\left(\sqrt{xy}+\sqrt{yz}+\sqrt{zx}\right)^2=25\)
\(\Leftrightarrow xy+yz+zx+2\left(\sqrt{xy^2z}+\sqrt{xyz^2}+\sqrt{x^2yz}\right)=25\)
\(\Leftrightarrow\sqrt{xyz}\left(\sqrt{x}+\sqrt{y}+\sqrt{z}\right)=8\Leftrightarrow\sqrt{xyz}=\frac{8}{4}\Leftrightarrow xyz=4\)(5)
Vậy hệ đã cho tương đương với :
\(\hept{\begin{cases}x+y+z=6\left(1\right)\\xy+yz+zx=9\left(4\right)\\xyz=4\left(5\right)\end{cases}}\)
Từ (5) \(\Rightarrow yz=\frac{4}{x}\)(Dễ thấy \(x,y,z>0\))
(4) \(\Leftrightarrow xy+yz+zx+x^2=9+x^2\Leftrightarrow x\left(x+y+z\right)+yz=9+x^2\)
\(\Leftrightarrow x.6+\frac{4}{x}=9+x^2\Leftrightarrow x^3-6x^2+9x-4=0\)
\(\Leftrightarrow\left(x-1\right)^2\left(x-4\right)=0\Leftrightarrow\orbr{\begin{cases}x=1\\x=4\end{cases}.}\)
Thế vào ta suy ra hệ có các nghiệm : \(\left(x,y,z\right)=\left(1,1,4\right),\left(1,4,1\right),\left(4,1,1\right).\)

Bài 1: ĐKXĐ: $2\leq x\leq 4$
PT $\Leftrightarrow (\sqrt{x-2}+\sqrt{4-x})^2=2$
$\Leftrightarrow 2+2\sqrt{(x-2)(4-x)}=2$
$\Leftrightarrow (x-2)(4-x)=0$
$\Leftrightarrow x-2=0$ hoặc $4-x=0$
$\Leftrightarrow x=2$ hoặc $x=4$ (tm)
Bài 2:
PT $\Leftrightarrow 4x^3(x-1)-3x^2(x-1)+6x(x-1)-4(x-1)=0$
$\Leftrightarrow (x-1)(4x^3-3x^2+6x-4)=0$
$\Leftrightarrow x=1$ hoặc $4x^3-3x^2+6x-4=0$
Với $4x^3-3x^2+6x-4=0(*)$
Đặt $x=t+\frac{1}{4}$ thì pt $(*)$ trở thành:
$4t^3+\frac{21}{4}t-\frac{21}{8}=0$
Đặt $t=m-\frac{7}{16m}$ thì pt trở thành:
$4m^3-\frac{343}{1024m^3}-\frac{21}{8}=0$
$\Leftrightarrow 4096m^6-2688m^3-343=0$
Coi đây là pt bậc 2 ẩn $m^3$ và giải ta thu được \(m=\frac{\sqrt[3]{49}}{4}\) hoặc \(m=\frac{-\sqrt[3]{7}}{4}\)
Khi đó ta thu được \(x=\frac{1}{4}(1-\sqrt[3]{7}+\sqrt[3]{49})\)

\(\hept{\begin{cases}x-\frac{12}{4}=y-\frac{9}{3}=z-1\left(1\right)\\3x+5y-z=2\left(2\right)\end{cases}}\)
từ (1), ta có: \(x-\frac{12}{4}=y-\frac{9}{3}\Rightarrow y=x-\frac{12}{4}+\frac{9}{3}=x\Rightarrow y=x\)
lại có: \(x-\frac{12}{4}=z-1\Rightarrow z=x-\frac{12}{4}+1=x-2\Rightarrow z=x-2\)
từ (2), ta rút y, z theo x, ta được: \(3x+5x-x+2=2\Rightarrow7x=0\Rightarrow x=y=0\)
\(\Rightarrow z=x-2=0-2=-2\)
vậy (x;y;z)=(0;0;-2)

\(\hept{\begin{cases}x+y-z=7\\x^2+y^2-z^2=37\\x^3+y^3-z^3=1\end{cases}}\)<=> \(\hept{\begin{cases}x+y=7+z\\x^2+y^2=37+z^2\\x^3+y^3=1+z^3\end{cases}}\)
Ta có: \(x^2+y^2=37+z^2\)
<=> \(\left(x+y\right)^2-2xy=37+z^2\)
<=> \(2xy=\left(7+z\right)^2-37-z^2\)
<=> \(xy=6+7z\)
Ta có: \(x^3+y^3=1+z^3\)
<=> \(\left(x+y\right)\left(x^2+y^2-xy\right)=1+z^3\)
<=> \(\left(7+z\right)\left(37+z^2-6-7z\right)=1+z^3\)đây là phương trình bậc 2. Em giải ra tìm z => x; y

\(\hept{\begin{cases}x+y+z=3\left(1\right)\\\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{1}{3}\left(2\right)\\x^2+y^2+z^2=17\left(3\right)\end{cases}}\left(DK:x,y,z\ne0\right)\)
Ta co:
\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\ge\frac{9}{x+y+z}=3>\frac{1}{3}\)
\(\Rightarrow\frac{1}{x}+\frac{1}{y}+\frac{1}{z}>\frac{1}{3}\)
Vay HPT vo nghiem

Lời giải:
$x,y,z>0$ thì $\frac{1}{x}, \frac{1}{y}, \frac{1}{z}$ mới xác định.
Áp dụng BĐT AM-GM:
$(x+y+z)(\frac{1}{x}+\frac{1}{y}+\frac{1}{z})\geq 3\sqrt[3]{xyz}.3\sqrt[3]{\frac{1}{xyz}}=9$
Dấu "=" xảy ra khi $x=y=z$. Thay vào pt $(2)$:
$x^3=x^2+x+2$
$\Leftrightarrow x^3-x^2-x-2=0$
$\Leftrightarrow x^2(x-2)+x(x-2)+(x-2)=0$
$\Leftrightarrow (x^2+x+1)(x-2)=0$
Dễ thấy $x^2+x+1>0$ với mọi $x>0$ nên $x-2=0$
$\Rightarrow x=2$
Vậy hpt có nghiệm $(x,y,z)=(2,2,2)$
Đưa hệ phương trình về dạng hệ tam giác bằng cách khử dần các ẩn.
Nhân phương trình (2) với 2 rồi cộng với phương trình (1) và cộng phương trình (2) với phương trình (3) ta được:
Giải hệ phương trình trên ta được
Vậy hệ phương trình có nghiệm