Cho hình thang ABCD (AB//CD) và AB < CD. Gọi E là điểm bất kỳ trên cạnh AB. Xác định vị trí điểm F trên cạnh CD để SAEFD v = SBCFE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: AE+EB=AB
BF+FC=BC
CG+GD=CD
DH+HA=DA
mà AB=BC=CD=DA và AE=BF=CG=DH
nên EB=FC=GD=HA
Xét ΔEAH vuông tại A và ΔGCF vuông tại C có
EA=GC
AH=CF
Do đó: ΔEAH=ΔGCF
=>EH=GF
Xét ΔEBF vuông tại B và ΔGDH vuông tại D có
EB=GD
BF=DH
Do đó: ΔEBF=ΔGDH
=>EF=GH
Xét ΔEAH vuông tại A và ΔFBE vuông tại B có
EA=FB
AH=BE
Do đó: ΔEAH=ΔFBE
=>EH=EF và \(\widehat{AEH}=\widehat{BFE}\)
\(\widehat{AEH}+\widehat{HEF}+\widehat{BEF}=180^0\)
=>\(\widehat{BFE}+\widehat{BEF}+\widehat{HEF}=180^0\)
=>\(\widehat{HEF}+90^0=180^0\)
=>\(\widehat{HEF}=90^0\)
Xét tứ giác EHGF có
EF=GH
EH=GF
Do đó: EHGF là hình bình hành
Hình bình hành EHGF có EF=EH
nên EHGF là hình thoi
Hình thoi EHGF có \(\widehat{HEF}=90^0\)
nên EHGF là hình vuông
b:
AH+HD=AD
=>AH+1=4
=>AH=3(cm)
ΔAEH vuông tại A
=>\(AE^2+AH^2=EH^2\)
=>\(EH^2=3^2+1^2=10\)
=>\(EH=\sqrt{10}\left(cm\right)\)
EHGF là hình vuông
=>\(S_{EHGF}=EH^2=10\left(cm^2\right)\)

Vì AB//CD (gt) -> \(\widehat{ABD}=\widehat{BDE}\) ( 2 góc so le trong )
Xét \(\Delta\)ABI và \(\Delta\)EDI có:
\(\widehat{ABD}=\widehat{BDE}\left(cmt\right)\)
DI=IB (I là trung điểm của BD)
\(\widehat{AIB}=\widehat{DIE}\) ( 2 góc đối đỉnh )
=> \(\Delta\)ABI = \(\Delta\)EDI ( g.c.g )
=> AB = DE ( 2 cạnh tương ứng ) (1)
Mà AB//DE ( AB//DC, E thuộc DC ) (2)
Từ (1) và (2) -> ABED là hình bình hành
-> AE cắt DB tại trung điểm mỗi đường ( tính chất hình bình hành ) mà I là trung điểm của BD
-> I là trung điểm AE
Chúc bạn học tốt!!!

a) Xét tứ giác ABED có
AB//ED(gt)
AB=ED
Do đó: ABED là hình bình hành(Dấu hiệu nhận biết hình bình hành)

Đáp án D
![]()
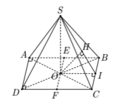
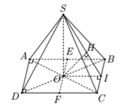
I là trung điểm cạnh đáy BC. Do SA = SB = SC = SD nên SO ⊥ (ABCD)
Từ đó ta chứng minh được
![]()
![]()
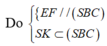
![]()
Tính được
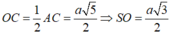
Suy ra
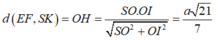
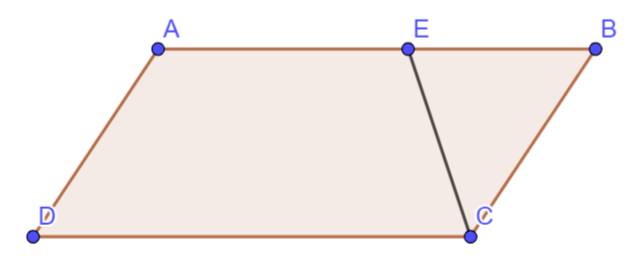
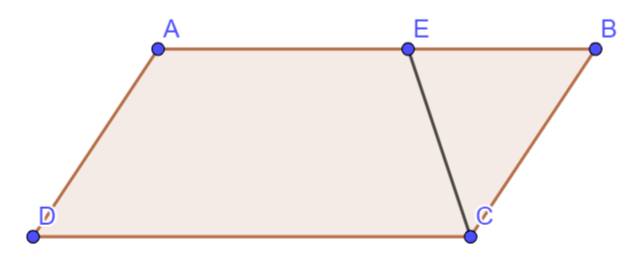

Do hình thang AEFD và hình thang BCFE có cùng đường cao, suy ra S A E F D = S B C F E ⇔ D F = A B + D C 2 − A E
Cách dựng: Vẽ đường trung bình MN, trên đó lấy MK = AE. Từ K vẽ đường song song với BC cắt CD tại F cần tìm