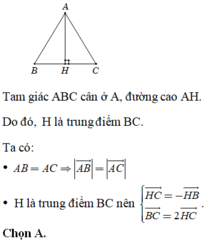
Cho tam giác ABC cân ở A, đường cao AH. Khẳng định nào sau đây sai?
A. A B → = A C → .
B. H C → = − H B → .
C. A B → = A C → .
D. B C → = 2 H C → .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
15 tháng 3 2018
Đúng(0)
Những câu hỏi liên quan
PT
1
CM
3 tháng 8 2017
Chọn A.
Tam giác ABC cân tại A, đường cao AH. Do đó, H là trung điểm BC.
Ta có:
+ tam giác cân tại A nên 
+ Do H là trung điểm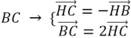 
CM
5 tháng 4 2017
Tam giác ABC cân tại A, đường cao AH.
Do đó, H là trung điểm BC.
Ta có:
AB = AC → A B → = A C →
+ Do H là trung điểm
→ H C → = - H B → B C → = 2 H C →
Chọn A
CM
24 tháng 10 2017
Do Tam giác ABC cân tại A, AH là đường cao nên H là trung điểm BC.
+Đáp án A. Ta có
CM
18 tháng 4 2017
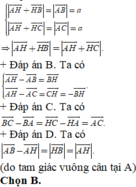
Chọn D.
+) Ta có :
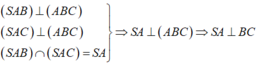
⇒ Suy ra : A đúng.
+) Ta có :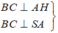 
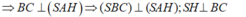
⇒ Suy ra : C đúng.
+) Mặt khác : AH ⊥ CD nên:
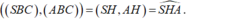
⇒ Suy ra : D sai.
CM
18 tháng 1 2019
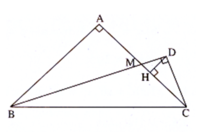
Theo câu a), từ AB = 2AM, suy ra HC = 2HD. Ta có HC < MC (h là chân đường cao hạ từ D của tam giác DCM vuông tại D) nên HC = 2HD < MC = AM < AH (do M nằm giữa A và H), vì thế 2HD không thể bằng AH. Khẳng định b) là sai.
CM
11 tháng 1 2019
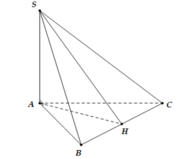
Chọn B.
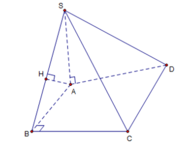
+) Vì tam giác ABC vuông tại B nên BC ⊥ AB.
- Lại có:
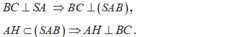
+) Theo gt AH ⊥ SB vậy:
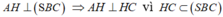
- Do đó AH không thể vuông góc với AC.(Một tam giác không thể có đồng thời hai góc vuông)
17 tháng 7
Cho tam giác ABC vuông tại A có AB < AC. Đường cao AH. Khẳng định nào sau đây sai?
A. HC < AC
B. AH < AC
C. BH > HC
D. BC > AC