Gọi x0 là nghiệm nguyên của phương trình 5 x . 8 x x + 1 = 100 . Tính giá trị của biểu thức P = x0(5 - x0)( x0 + 8).
A.40
B.50
C.60
D.70
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1
1
10 tháng 1 2022
\(x_0=\dfrac{10}{3}\)
\(\Leftrightarrow Q=3\cdot\dfrac{10}{3}-2=10-2=8\)
CM
17 tháng 5 2018
Ta có d: −2x + y = 3 ⇔ y = 2x + 3 và d’: x + y = 5 ⇔ y = 5 – x
Xét phương trình hoành độ giao điểm của d và d’: 2x + 3 = 5 – x ⇔ x = 2 3
⇒ y = 5 – x = 5 − 2 3 = 13 3
Vậy tọa độ giao điểm của d và d’ là 2 3 ; 13 3
Suy ra nghiệm của hệ phương trình − 2 x + y = 3 x + y = 5 là 2 3 ; 13 3
Từ đó y 0 – x 0 = 13 3 − 2 3 = 11 3
Đáp án: A
CM
16 tháng 9 2017
Số 2 lớn hơn mọi giá trị khác của hàm số f(x) = sinx với tập xác định D = R nhưng 2 không phải là giá trị lớn nhất của hàm số này (giá trị lớn nhất là 1); vì vậy A sai. Cũng như vậy B sai với f(x) = sinx, D = R, M = 2. Phát biểu C tự mâu thuẫn: vì M = f( x 0 ), x 0 ∈ D nên hay không xảy ra M > f(x), ∀x ∈ D.
Đáp án: D
CM
11 tháng 3 2018
Giá x 0 thỏa mãn A( x 0 ) = B( x 0 ) được gọi là nghiệm của phương trình A(x) = B(x)
Đáp án cần chọn là: D
AH
Akai Haruma
Giáo viên
11 tháng 9 2021
Lời giải:
a. Tại $x_0=\sqrt{5}$ thì:
$y=f(x_0)=\frac{x_0}{2}-\sqrt{x_0^2-1}+2$
$=\frac{\sqrt{5}}{2}-\sqrt{5-1}+2=\frac{\sqrt{5}}{2}$
b. Tại $x=\frac{1}{4}$ thì $x^2-1=\frac{-15}{16}< 0$ nên căn thức $\sqrt{x^2-1}$ không xác định. Do đó không tính được.
CM
4 tháng 2 2019
Đáp án A
Đặt t = sin x + cos x = 2 sin x + π 4 ∈ - 2 ; 2 ⇒ sin x cos x = t 2 - 1 2
Khi đó sin x cos x + 2 sin x + cos x = 2 ⇔ t 2 - 1 2 + 2 t = 2 ⇔ t 2 + 4 t - 5 = 0 ⇔ t = 1
Vậy P = sin x 0 + π 4 = sin x 0 + cos x 0 2 = t 0 2 = 2 2 .
Chọn C.
Điều kiện. x ≠ -1
Phương trình tương đương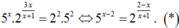
Lấy ln hai vế của , ta được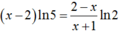
Suy ra x0 = 2 và P = 60.
= x0(5 - x0)( x0 + 8).