Cho phương trình 2016 x 2 - 1 + x 2 - 1 . 2017 x = 1 . Mệnh đề nào sau đây là đúng?
A. Phương trình đã cho có tổng các nghiệm bằng 0.
B. Phương trình đã cho có nghiệm duy nhất.
C. Phương trình đã cho có hai nghiệm dương phân biệt.
D. Phương trình đã cho có nhiều hơn hai nghiệm.


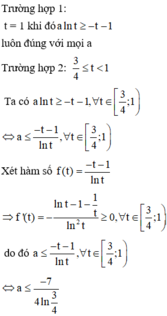
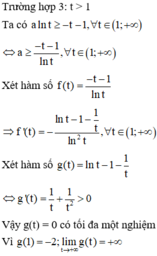
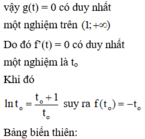
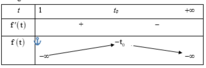



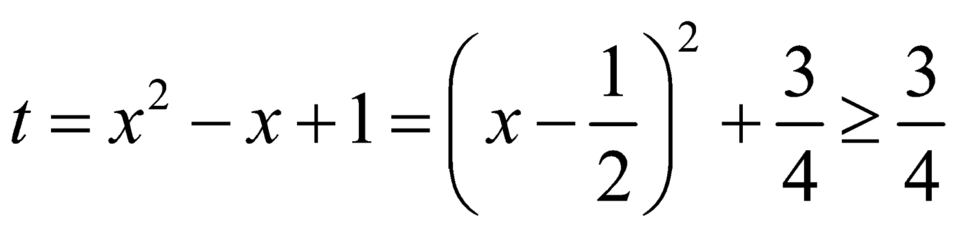
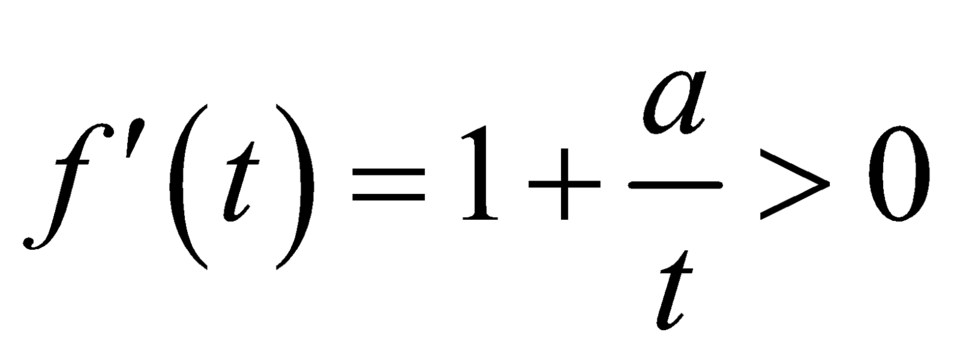
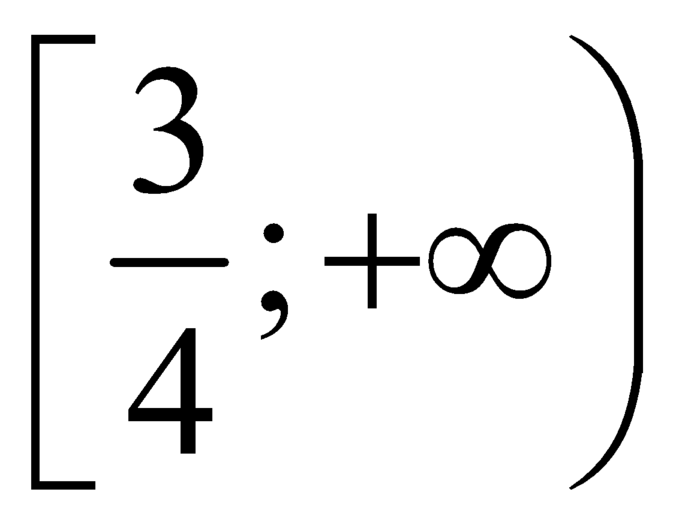 .
.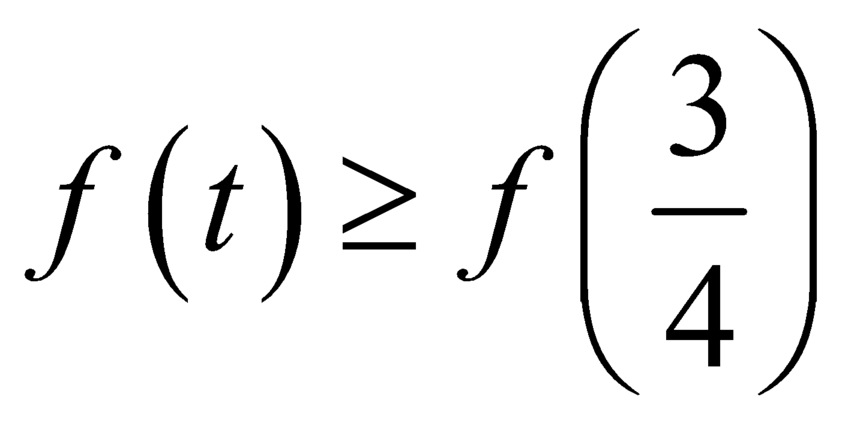
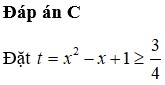


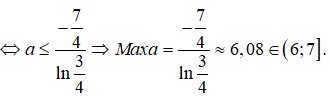



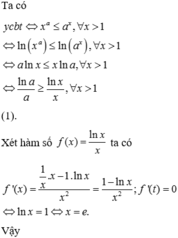
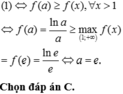
Chọn A.
+Nếu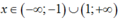 thì x2 – 1 > 0. Suy ra
thì x2 – 1 > 0. Suy ra 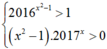
+ Nếu -1 < x < 1 thì x2 - 1 < 0. Suy ra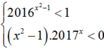
+ Kiểm tra x = 1 ; x = -1 thỏa mãn phương trình đã cho.
Vậy phương trình đã cho có hai nghiệm x = -1 ; x = 1.
Suy ra phương trình đã cho có tổng các nghiệm bằng 0.