Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\7^x\ge m\end{matrix}\right.\)
\(\left[{}\begin{matrix}4log_2^2x+log_2x-5=0\\7^x-m=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x_1=2\\x_2=2^{-\dfrac{5}{4}}\\7^x=m\end{matrix}\right.\)
Với \(m\le0\) thì pt đã cho luôn có đúng 2 nghiệm
Vậy không cần xét tiếp, hiển nhiên là có vô số giá trị thực của m rồi?

Đáp án B
P T ⇔ log 2 2 x 2 - x + 2 m - 4 m 2 + log 2 x 2 + m x - 2 m 2 = 0
⇔ 2 x 2 - x + 2 m - 4 m 2 = x 2 + m x - 2 m 2 > 0
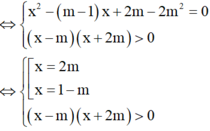
Điều kiện để pt đã cho có 2 nghiệm
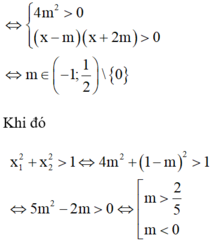
Do đó
S = - 1 ; 0 ∪ 2 5 ; 1 2 ⇒ A = - 1 + 2 + 1 = 2

Đáp án B.
Đặt t = log2 x,
khi đó m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0
⇔ m + 1 t 2 + 2 t + m - 2 = 0 (*).
Để phương trình (*) có hai nghiệm phân biệt
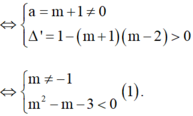
Khi đó gọi x1, x2 lần lượt hai nghiệm của phương trình (*).
Vì 0 < x1 < 1 < x2 suy ra
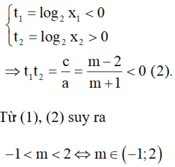

Chọn D.
Phương trình ![]()
Ta thấy 1 - (m + 3) + m + 2 = 0 nên 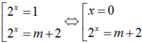
Từ đó 2x = m + 2 cần phải có nghiệm thực khác 0 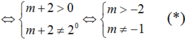
Khi đó 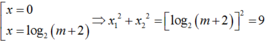
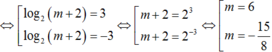 thỏa mãn (*)
thỏa mãn (*)
Kết hợp với m > 0 đề bài cho thì ta được m = 6 thỏa mãn.





Chọn A.
+Nếu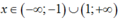 thì x2 – 1 > 0. Suy ra
thì x2 – 1 > 0. Suy ra 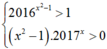
+ Nếu -1 < x < 1 thì x2 - 1 < 0. Suy ra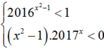
+ Kiểm tra x = 1 ; x = -1 thỏa mãn phương trình đã cho.
Vậy phương trình đã cho có hai nghiệm x = -1 ; x = 1.
Suy ra phương trình đã cho có tổng các nghiệm bằng 0.