Những điểm cách điểm 0 bốn đơn vị là A. 4 và −4 B. 2 và −2 C. 2 và 4 ...
Đọc tiếp
Những điểm cách điểm 0 bốn đơn vị là
A. 4 và −4
B. 2 và −2
C. 2 và 4
D. 4 và −2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 10 2019
a. Các điểm A, B, C, D tương ứng biểu diễn các số: + 2; + 4; - 2; - 3;
b. A và C cách đều O; O và B cách đều A;
c. Hai điểm C và O nằm giữa hai điểm A và D.
19 tháng 5 2017
Trục số:
a) Những điểm nằm cách điểm 2 ba đơn vị: -1; 5
b) Những điểm nằm giữa các điểm -3 và 4: -2; -1; 0; 1; 2; 3
27 tháng 12 2017
a) Những điểm nằm cách điểm 2 ba đơn vị: -1; 5
b) Những điểm nằm giữa các điểm -3 và 4: -2; -1; 0; 1; 2; 3
2
10 tháng 5 2022
Có: `x-2y+4=0`
`<=>x=2y-4`
Thay `x=2y-4` vào `(E)` có:
`3(2y-4)^2+4y^2-48=0`
`<=>3(4y^2-16y+16)+4y^2-48=0`
`<=>12y^2-48y+48+4y^2-48=0`
`<=>` $\left[\begin{matrix} y=3\\ y=0\end{matrix}\right.$
`@y=3=>x=2.3-4=2`
`@y=0=>x=2.0-4=-4`
`=>` Tọa độ giao điểm của `(E)` và `(d)` là: `(2;3)` và `(-4;0)`
`->D`
10 tháng 5 2022
\(\Rightarrow\) \(chọn\) \(D\)
\(xét\) \(hpt\) \(:\)
\(\left\{{}\begin{matrix}3x^2+4y^2-48=0\\x-2y+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3\left(2y-4\right)^2+4y^2-48=0\\x=2y-4\end{matrix}\right.\)
\(giải:\) \(3\left(4y^2-16y+16\right)+4y^2-48=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}12y^2-48y+48+4y^2-48=0\\16y^2-48y=0\\\left[{}\begin{matrix}y=0\Rightarrow x=-4\\y=3\Rightarrow x=2\end{matrix}\right.\end{matrix}\right.\)
\(vậy\) \(giao\) \(điểm\) \(của\) \(elip\) \(\left(E\right)\) \(là\) \(\left(-4;0\right)\) \(và\) \(\left(2;3\right)\)
CM
17 tháng 10 2018
Đáp án D
+ Đường thẳng AB có vectơ chỉ phương là A B → ( - 1 ; 2 ) và đường thẳng CD có vectơ chỉ phương là C D → ( - 2 ; 4 ) . .
+ Ta thấy A B → v à C D → cùng phương nên AB và CD không có giao điểm.
CM
13 tháng 12 2018
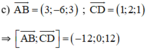
(α) chứa AB và song song với CD
⇒ (α) nhận (1; 0; -1) là 1 vtpt
(α) đi qua A(-2; 6; 3)
⇒ (α): x – z + 5 = 0.
Đáp án cần chọn là: A
Điểm nằm bên phải điểm 0 và cách điểm 0 bốn đơn vị là: 4
Điểm nằm bên trái điểm 0 và cách điểm 0 bốn đơn vị là: −4.