Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, S A ⊥ ( A B C S ) , S A = a Gọi G là trọng tâm tam giác SCD. Tính thể tích khối chóp G.ABCD
A. 1/6a3
B. 1/12a3
C. 2/17a3
D. 1/9a3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án C
Phương pháp giải:
Xác định hình chiếu của đỉnh, xác định góc để tìm chiều cao và áp dụng công thức thể tích
Lời giải:
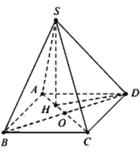
Gọi O là tâm hình vuông ABCD , H là trọng tâm tam giác ABD
Ta có ![]()
![]()
ABCD là hình vuông cạnh a nên 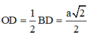
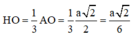
Tam giác HDO vuông tại O, có 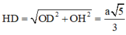
Tam giác SHD vuông tại H, có 
Vậy thể tích cần tính là 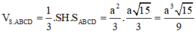

Đáp án D.
Phương pháp:
- Xác định chân đường cao của đỉnh S đến mặt phẳng đáy.
- Tính thể tích khối chóp: V = 1 3 S h
Cách giải:
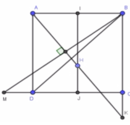
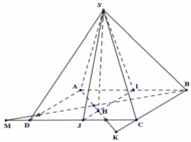
Gọi I, J lần lượt là trung điểm của AB, CD.
Tam giác SAB đều, tam giác SCD cân tại S nên S I ⊥ A B , S J ⊥ C D
Mà A B / / C D ⇒ A B , C D ⊥ S IJ
Dựng S H ⊥ I J , H ∈ I J ⇒ S H ⊥ A B C D (do S H ⊥ I J và S H ⊂ SIJ ⊥ C D )
Trong (ABCD), kẻ
B M ⊥ A H , M ∈ C D , A H ∩ B M = T .
Khi đó, điểm M thỏa mãn điều kiện đề bài.
+) Δ S A B đều, cạnh a ⇒ S I = a 3 2
+) Δ S C D vuông cân tại S,
C D = a ⇒ S J = C D 2 = a 2
+) ABCD là hình vuông cạnh a
⇒ IJ = a
Tam giac SIJ có:
IJ 2 = S I 2 + S J 2 ⇒ Δ S I J vuông tại S.
Mà
S H ⊥ IJ ⇒ SI 2 = I H . IJ ⇒ a 3 2 2 = I H . a ⇒ I H = 3 a 4
Và
1 S H 2 = 1 S I 2 + 1 S J 2 = 1 a 3 2 2 + 1 a 2 2 = 16 3 a 2 ⇒ S H = a 3 4
Dễ dàng chứng minh Δ A I H đồng dạng tam giác
Δ B C M ⇒ S A I H S B M C = A I B C 2 = 1 4 ⇒ S B C M = 4 S A I H = 4. 1 2 . a 2 . 3 a 4 = 3 a 2 4
S B D M = S B C M − S B C D = 3 4 a 2 − 1 2 a 2 = a 2 4
Thể tích khối chóp S.BDM:
V S . B D M = 1 3 . S H . S B D M = 1 3 . a 3 4 . a 2 4 = 3 a 3 48