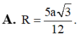
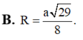
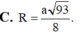
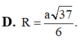
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
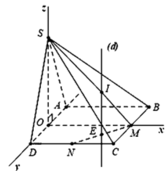
Xét trục tọa độ Oxyz như hình vẽ, với O là trung điểm của AD
Chọn a = 1 =>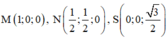 
=> Trung điểm của MN là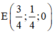 
Phương trình đường thẳng qua E, song song với Oz là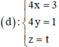 
Gọi I là tâm mặt cầu cần tìm =>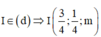 
Suy ra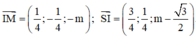 
Mà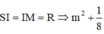 
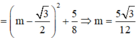
Vậy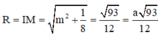 
Đáp án C.
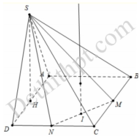
Chọn hệ trục tọa độ với H ≡ O 0 ; 0 ; 0 D 1 2 ; 0 ; 0 . Chọn a = 1.
M 0 ; 1 ; 0 ; N 1 2 ; 1 2 ; 0 ; S 0 ; 0 ; 3 2 ; C 1 2 ; 1 ; 0 là: x = 1 4 y = 3 4 z = t ⇒ tâm mặt cầu có tọa độ K 1 4 ; 3 4 ; t
Giải:
S K = K C ⇔ 1 16 + 9 16 + t − 3 2 2 = 1 16 + 1 16 + t 2 ⇔ t = 5 3 12 ⇒ R = K C = 93 12 .
Chọn D.
Áp dụng công thức tìm nhanh bán kính mặt cầu ngoại tiếp hình chóp R 2 = x 2 + r 2 với
r là bán kính đường tròn ngoại tiếp đa giác đáy
x = S O 2 - r 2 2 h : S là đỉnh hình chóp , O là tâm đường tròn ngoại tiếp đa giác đáy, h là chiều cao hình chóp
Cụ thể vào bài toán:
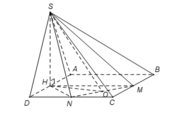
Đáy là tam giác CMN vuông tại C
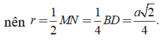
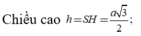
Tâm O của đường tròn ngoại tiếp tam giác CMN là trung điểm MN
Áp dụng công thức đường trung tuyến trong tam giác HMN tính được H O 2 = 5 a 2 8
Trong tam giác vuông SHO có
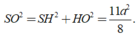
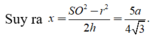
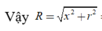
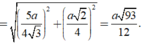
Đáp án C.
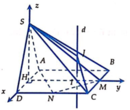
Gọi H là trung điểm của AD 
Cho hệ trục tọa độ như hình vẽ => 
Trung điểm MN là 
có 
Gọi d là đường thẳng đi qua I và vuông góc với (ABCD)
=> d có vecto chỉ phương 
∆ NCM vuông tại C => I là tâm đường tròn ngoại tiếp
=> d là trục của đường tròn ngoại tiếp tam giác CMN
=> Tâm J của mặt cầu ngoại tiếp SCMN thuộc d
Ta có d qua 
và 
là vecto chỉ phương
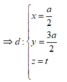
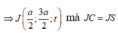
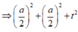
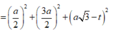
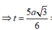=> Bán kính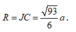 
Đáp án C
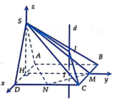
Gọi H là trung điểm của A D ⇒ S H ⊥ ( A B C D ) ⇒ S H = a 3
Cho hệ trục tọa độ như hình vẽ ⇒ D ( a ; 0 ; 0 ) , M ( 0 ; 2 a ; 0 ) , N ( a ; a ; 0 )
⇒ Trung điểm MN là I a 2 ; 3 a 2 ; 0 có S 0 ; 0 ; a 3 , C a ; 2 a ; 0
Gọi d là đường thẳng đi qua I và vuông góc với (ABCD)
⇒ d có vecto chỉ phương k → = 0 ; 0 ; 1
∆ N C M vuông tại C là tâm đường tròn ngoại tiếp
⇒ d là trục của đường tròn ngoại tiếp tam giác CMN
⇒ Tâm J của mặt cầu ngoại tiếp SCMN thuộc d
Ta có d qua I a 2 ; 3 a 2 ; 0 và k → = 0 ; 0 ; 1 là vecto chỉ phương ⇒ d : x = a 2 y = 3 a 2 z = t
⇒ J a 2 ; 3 a 2 ; t mà J C = J S ⇒ a 2 2 + a 2 2 + t 2 = a 2 2 + 3 a 2 2 + a 3 - t 2
⇒ t = 5 a 3 6 Bán kính R = J C = 93 6 a .
