Cho các phân thức x − 3 2 x 2 − 3 x − 2 và 2 x − 1 x 2 + x − 6 với x ≠ − 3 ; x ≠ − 1 2 và x ≠ 2 . Không dùng cách phân tích các mẫu thức thành nhân tử, hãy chứng tỏ rằng có thể quy đồng mẫu thức hai phân thức này với mẫu thức chung là N = 2 x 3 + 3 x 2 − 11 x − 6 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

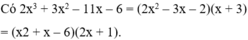

a: \(\dfrac{x^2-4x+4}{x^2-2x}=\dfrac{\left(x-2\right)^2}{x\left(x-2\right)}=\dfrac{x-2}{x}=\dfrac{\left(x-2\right)\left(x-1\right)}{x\left(x-1\right)}\)
\(\dfrac{x+1}{x^2-1}=\dfrac{1}{x-1}=\dfrac{x}{x\left(x-1\right)}\)
b: \(\dfrac{x^3-2^3}{x^2-4}=\dfrac{x^2+2x+4}{x+2}\)
3/x+2=3/x+2

\(a,\dfrac{x^3-2^3}{x^2-4}=\dfrac{\left(x-2\right)\left(x^2-2x+4\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{x^2-2x+4}{x+2}\\ b,\dfrac{2}{2x-4}=\dfrac{2}{2\left(x-2\right)}=\dfrac{1}{x-2}\\ \dfrac{3}{3x-6}=\dfrac{3}{3\left(x-2\right)}=\dfrac{1}{x-2}\)

1.
\(A=\dfrac{2x-9}{\left(x-2\right)\left(x-3\right)}-\dfrac{\left(x-3\right)\left(x+3\right)}{\left(x-2\right)\left(x-3\right)}+\dfrac{\left(2x+4\right)\left(x-2\right)}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{2x-9-\left(x^2-9\right)+\left(2x^2-8\right)}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{x^2+2x-8}{\left(x-2\right)\left(x-3\right)}=\dfrac{\left(x-2\right)\left(x+4\right)}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{x+4}{x-3}\)
b.
\(A=2\Rightarrow\dfrac{x+4}{x-3}=2\Rightarrow x+4=2\left(x-3\right)\)
\(\Rightarrow x=10\) (thỏa mãn)
2.
\(x^4+2x^2y+y^2-9=\left(x^2+y\right)^2-3^2=\left(x^2+y-3\right)\left(x^2+y+3\right)\)

Bài 1:
a: \(A=\dfrac{x^2-3+x+3}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x+3}{x}=\dfrac{x\left(x+1\right)}{x\left(x-3\right)}=\dfrac{x+1}{x-3}\)
b: Để A=3 thì 3x-9=x+1
=>2x=10
hay x=5
Bài 2:
a: \(A=\dfrac{x+x-2-2x-4}{\left(x-2\right)\left(x+2\right)}:\dfrac{x+2-x}{x+2}\)
\(=\dfrac{-6}{x-2}\cdot\dfrac{1}{2}=\dfrac{-3}{x-2}\)
b: Để A nguyên thì \(x-2\in\left\{1;-1;3;-3\right\}\)
hay \(x\in\left\{3;1;5;-1\right\}\)

\(a.\) Ta có:
\(MTC:\) \(\left(x+1\right)\left(x+2\right)\)
Do đó
\(\frac{3x}{x+1}=\frac{3x\left(x+2\right)}{\left(x+1\right)\left(x+2\right)}\)
\(\frac{x+4}{x+2}=\frac{\left(x+1\right)\left(x+4\right)}{\left(x+1\right)\left(x+2\right)}\)
\(b.\) Ta có:
\(x^2+x=x\left(x+1\right)\)
\(x^2-1=\left(x-1\right)\left(x+1\right)\)
nên \(MTC:\) \(x\left(x-1\right)\left(x+1\right)\)
Do đó:
\(\frac{5}{x^2+x}=\frac{5}{x\left(x+1\right)}=\frac{5\left(x-1\right)}{x\left(x-1\right)\left(x+1\right)}\)
\(\frac{6}{x^2-1}=\frac{6}{\left(x-1\right)\left(x+1\right)}=\frac{6x}{x\left(x-1\right)\left(x+1\right)}\)
\(c.\) Ta có:
\(x^2-5x+4=x^2-x-4x+4=x\left(x-1\right)-4\left(x-1\right)=\left(x-1\right)\left(x-4\right)\)
\(2x^2-8x=2x\left(x-4\right)\)
nên \(MTC:\) \(2x\left(x-1\right)\left(x-4\right)\)
Do đó:
\(\frac{4}{x^2-5x+4}=\frac{4}{\left(x-1\right)\left(x-4\right)}=\frac{8x}{2x\left(x-1\right)\left(x-4\right)}\)
\(\frac{x+1}{2x^2-8x}=\frac{x+1}{2x\left(x-4\right)}=\frac{\left(x-1\right)\left(x+1\right)}{2x\left(x-1\right)\left(x-4\right)}\)
Làm nốt d :P
\(\frac{x+3}{2x^2-15x-8};\frac{3}{x^2-8x}\)
Ta có : \(2x^2-15x-8=\left(2x+1\right)\left(x-8\right)\)
\(x^2-8x=x\left(x-8\right)\)
MTC : \(x\left(x-8\right)\left(2x+1\right)\)
\(\frac{x+3}{2x^2-15x-8}=\frac{x+3}{\left(2x+1\right)\left(x-8\right)}=\frac{x^2+3x}{x\left(x-8\right)\left(2x+1\right)}\)
\(\frac{3}{x^2-8x}=\frac{3}{x\left(x-8\right)}=\frac{6x+3}{x\left(x-8\right)\left(2x+1\right)}\)