cho tam giác ABC vuông tại A,AD là đường phân giác qua D vẽ DE⊥AB(E thuộc AB)DF⊥AC (F thuộc AC). Chứng minh AEDF là hình vuông
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét tứ giác AEDF có
DE//AF
AE//DF
Do đó: AEDF là hình bình hành
mà \(\widehat{DAE}=90^0\)
nên AEDF là hình chữ nhật
mà AD là tia phân giác
nên AEDF là hình vuông

a: Xét tứ giác AEDF có
AE//DF
DE//AF
Do đó: AEDF là hình bình hành
mà \(\widehat{DAE}=90^0\)
nên AEDF là hình chữ nhật
a, Vì DE//AB nên DE⊥AC và DF//AC nên DF⊥AB
Vì \(\widehat{AED}=\widehat{AFD}=\widehat{EAF}=90^0\) nên AEDF là hcn
b,Vì E là trung điểm MD và AC nên AMCD là hbh
Mà AC⊥DE nên AMCD là hthoi
c, Vì D là trung điểm BC và AK và \(\widehat{BAC}=90^0\) nên ABKC là hcn
Để ABKC là hv thì AB=AC hay tam giác ABC vuông cân tại A

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
b: Xét ΔABC có
D là trung điểm của BC
DE//AC
Do đó: E là trung điểm của AB
Xét tứ giác AIBD có
E là trung điểm của AB
E là trung điểm của ID
Do đó: AIBD là hình bình hành
mà AB\(\perp\)DI
nên AIBD là hình thoi

a: Xét tứ giác AEDF có
góc AED=góc AFD=góc FAE=90 độ
nên AEDF là hình chữ nhật
b: Xét ΔABC có CF/CA=CD/CB
nên DF//AB và DF=AB/2
=>Di//AB và DI=AB
=>ABDI là hình bình hành

a: Xét tứ giác AEDF có
\(\widehat{FAE}=\widehat{AFD}=\widehat{AED}=90^0\)
Do đó: AEDF là hình chữ nhật
mà AD là tia phân giác của \(\widehat{FAE}\)
nên AEDF là hình vuông

a) vận dụng định lý của lớp 6. DE//AB VÀ AB \(\perp\) AC => DE \(\perp\) AC
TƯƠNG TỰ DF \(\perp\) AB
=> HCN (3 GÓC VUÔNG)
b) vận dụng định lý đường trung bình => E là trung điểm của AC
=> DE = 1/2 AB = BF
=> BFED là HBH (1 cặp cạnh đối // và = nhau)
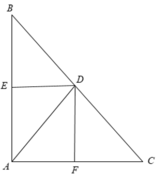

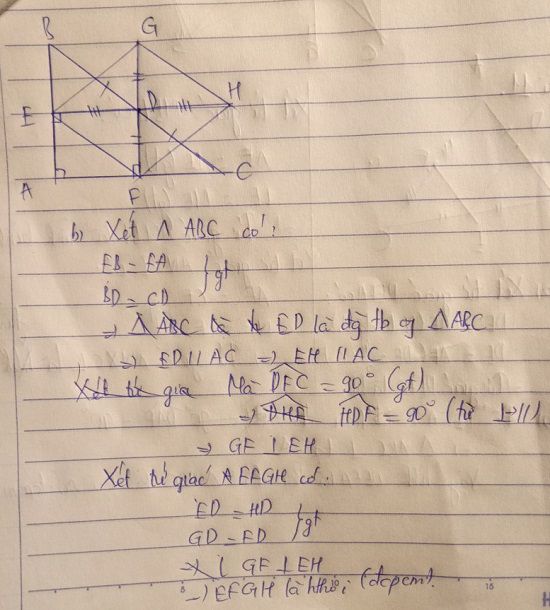

Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
mà AD là tia phân giác
nên AEDF là hình vuông