Tìm hàm số y=f(x) nếu biết dy = 6 x ( 3 x 2 - 1 ) 3 dx và f(0)=1
A. y = ( 3 x 2 - 1 ) 4 4 + 5 4
B. y = ( 3 x 2 - 1 ) 4 2 + 1 2
C. y = ( 3 x 2 - 1 ) 4 3 + 2 3
D. y = ( 3 x 2 - 1 ) 4 4 + 3 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

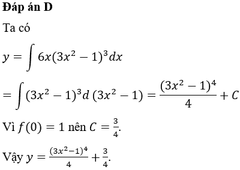

Câu 1:
a)
| \(y=f\left(x\right)=2x^2\) | -5 | -3 | 0 | 3 | 5 |
| f(x) | 50 | 18 | 0 | 18 | 50 |
b) Ta có: f(x)=8
\(\Leftrightarrow2x^2=8\)
\(\Leftrightarrow x^2=4\)
hay \(x\in\left\{2;-2\right\}\)
Vậy: Để f(x)=8 thì \(x\in\left\{2;-2\right\}\)
Ta có: \(f\left(x\right)=6-4\sqrt{2}\)
\(\Leftrightarrow2x^2=6-4\sqrt{2}\)
\(\Leftrightarrow x^2=3-2\sqrt{2}\)
\(\Leftrightarrow x=\sqrt{3-2\sqrt{2}}\)
hay \(x=\sqrt{2}-1\)
Vậy: Để \(f\left(x\right)=6-4\sqrt{2}\) thì \(x=\sqrt{2}-1\)

a ) Ta có : f(2) = 5
\(\Leftrightarrow\hept{\begin{cases}f\left(x\right)=f\left(2\right)\\\text{ax}-3=5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=2\\a.2-3=5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=2\\a=4\end{cases}}\)
Vậy a = 4
b ) Ta có : f(0) = 3
\(\Leftrightarrow\hept{\begin{cases}f\left(x\right)=f\left(0\right)\\\text{ax}+b=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=0\\a.0+b=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=0\\b=3\end{cases}}\) ( 1 )
Ta có : f ( 1 ) = 4
\(\Leftrightarrow\hept{\begin{cases}f\left(x\right)=f\left(1\right)\\\text{ax}+b=4\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1\\a.1+b=4\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1\\a+b=4\end{cases}}\) ( 2 )
Thay b = 3 ở ( 1 ) vào a+b=4 ở ( 2 ) ta được : a + 3 = 4
a = 1
Vậy a = 1 ; b = 3

Chọn C.
Đặt u = G ( x ) d v = f ( x ) d x ⇒ d u = G ( x ) ' d x = g ( x ) d x v = ∫ f ( x ) d x = F ( x )
Suy ra: I = G ( x ) F ( x ) 2 0 - ∫ 0 2 F ( x ) g ( x ) d x
= G(2)F(2) – G(0)F(0) – 3 = 1 – 0 – 3 = -2.

a: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{2}a\cdot\left(-4\right)+b=-3\\\dfrac{1}{2}a\cdot0+b=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2a+b=-3\\b=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-3\\a=0\end{matrix}\right.\)
Vậy: f(x)=-3
b: f(1)=f(2)=f(-2)=f(-1)=-3
c: Đặt y=4
=>f(x)=4
=>-3=4(vô lý)

\(f\left(x\right)=x^2-5x+6\)
a) +) \(f\left(-\frac{1}{3}\right)=\left(-\frac{1}{3}\right)^2-5.\left(-\frac{1}{3}\right)+6=\frac{70}{9}\)
+) \(f\left(\frac{1}{2}\right)=\left(\frac{1}{2}\right)^2-5.\frac{1}{2}+6=\frac{15}{4}\)
+) \(f\left(0\right)=0^2-5.0+6=6\)
+) \(f\left(1\right)=1^2-5.1+6=2\)
b) \(x^2-5x+6=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\x-3=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=2\\x=3\end{cases}}\)
ok