Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(f\left(0\right)=\dfrac{b}{d}\Rightarrow f\left(f\left(0\right)\right)=0\Rightarrow f\left(\dfrac{b}{d}\right)=0\)
\(\Rightarrow\dfrac{\dfrac{ab}{d}+b}{\dfrac{cb}{d}+d}=0\Rightarrow b\left(a+d\right)=0\Rightarrow\left[{}\begin{matrix}b=0\\d=-a\end{matrix}\right.\)
TH1: \(b=0\)
\(f\left(1\right)=1\Rightarrow a=c+d\)
\(f\left(2\right)=2\Rightarrow2a=2\left(2c+d\right)\Rightarrow a=2c+d\)
\(\Rightarrow2c+d=c+d\Rightarrow c=0\) (ktm)
TH2: \(d=-a\)
\(f\left(1\right)=1\Rightarrow a+b=c+d=c-a\Rightarrow2a+b=c\) (1)
\(f\left(2\right)=2\Rightarrow2a+b=2\left(2c+d\right)=2\left(2c-a\right)\Rightarrow4a+b=4c\) (2)
Trừ (2) cho (1) \(\Rightarrow2a=3c\Rightarrow\dfrac{a}{c}=\dfrac{3}{2}\)
\(\Rightarrow\lim\limits_{x\rightarrow\infty}\dfrac{ax+b}{cx+d}=\dfrac{a}{c}=\dfrac{3}{2}\)
Hay \(y=\dfrac{3}{2}\) là tiệm cận ngang

Lời giải:
Bài 1:
Ta nhớ công thức \(\sin^2x=\frac{1-\cos 2x}{2}\). Áp dụng vào bài toán:
\(F(x)=8\int \sin^2\left(x+\frac{\pi}{12}\right)dx=4\int \left [1-\cos \left(2x+\frac{\pi}{6}\right)\right]dx\)
\(\Leftrightarrow F(x)=4\int dx-4\int \cos \left(2x+\frac{\pi}{6}\right)dx=4x-2\int \cos (2x+\frac{\pi}{6})d(2x+\frac{\pi}{6})\)
\(\Leftrightarrow F(x)=4x-2\sin (2x+\frac{\pi}{6})+c\)
Giải thích 1 chút: \(d(2x+\frac{\pi}{6})=(2x+\frac{\pi}{6})'dx=2dx\)
Vì \(F(0)=8\Rightarrow -1+c=8\Rightarrow c=9\)
\(\Rightarrow F(x)=4x-2\sin (2x+\frac{\pi}{6})+9\)
Câu 2:
Áp dụng nguyên hàm từng phần như bài bạn đã đăng:
\(\Rightarrow F(x)=-xe^{-x}-e^{-x}+c\)
Vì \(F(0)=1\Rightarrow -1+c=1\Rightarrow c=2\)
\(\Rightarrow F(x)=-e^{-x}(x+1)+2\), tức B là đáp án đúng

Ta có bảng biến thiên như hình vẽ sau:
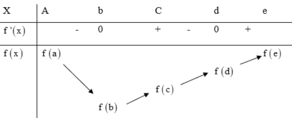
Giá trị nhỏ nhất của hàm số là f( b) nhưng giá trị lớn nhất có thể là f (a) hoặc f( e) Theo giả thiết ta có: f(a) + f( c)) = f( b) + f( d) nên f(a) - f( d)) = f( b) - f( c)< 0
Suy ra : f( a) < f( d) < f( e)
Vậy m a x [ a ; e ] f ( x ) = f ( e ) ; m i n [ a ; e ] f ( x ) = f ( b )
Chọn C.
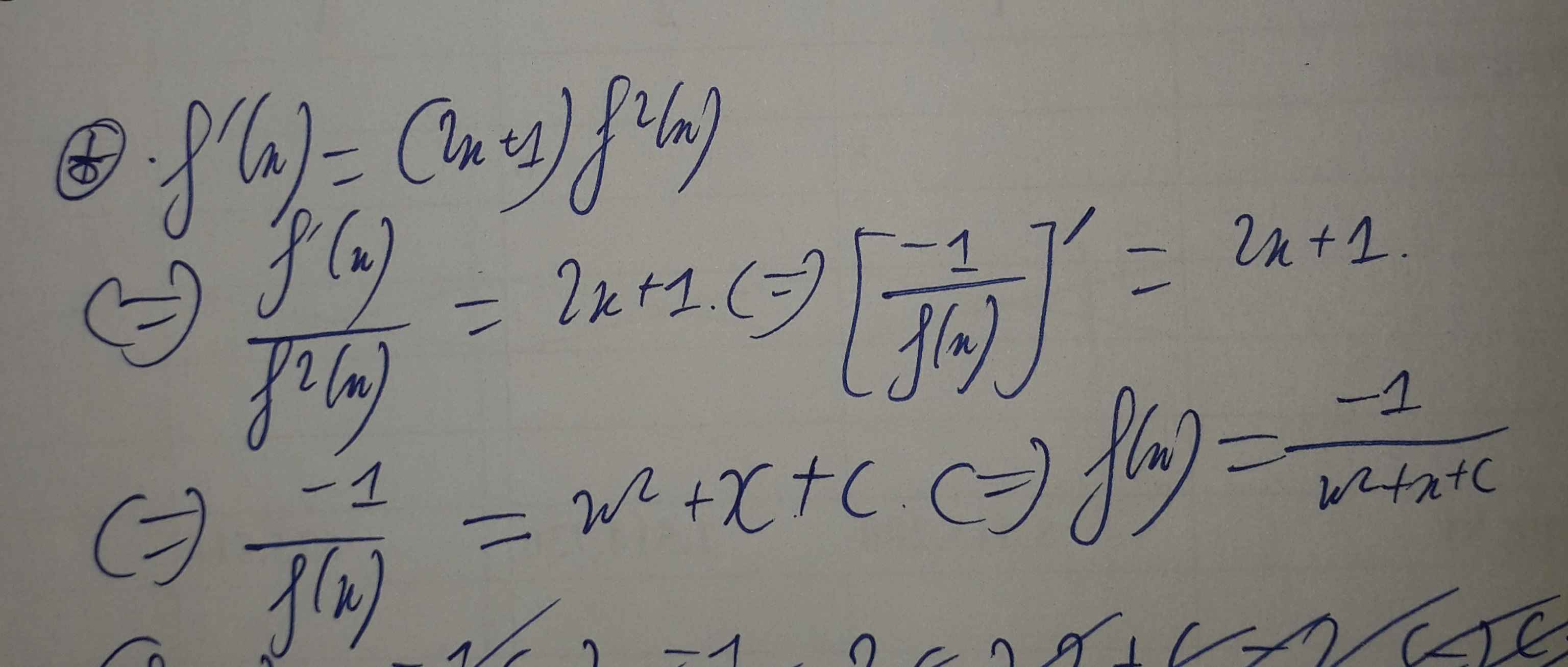
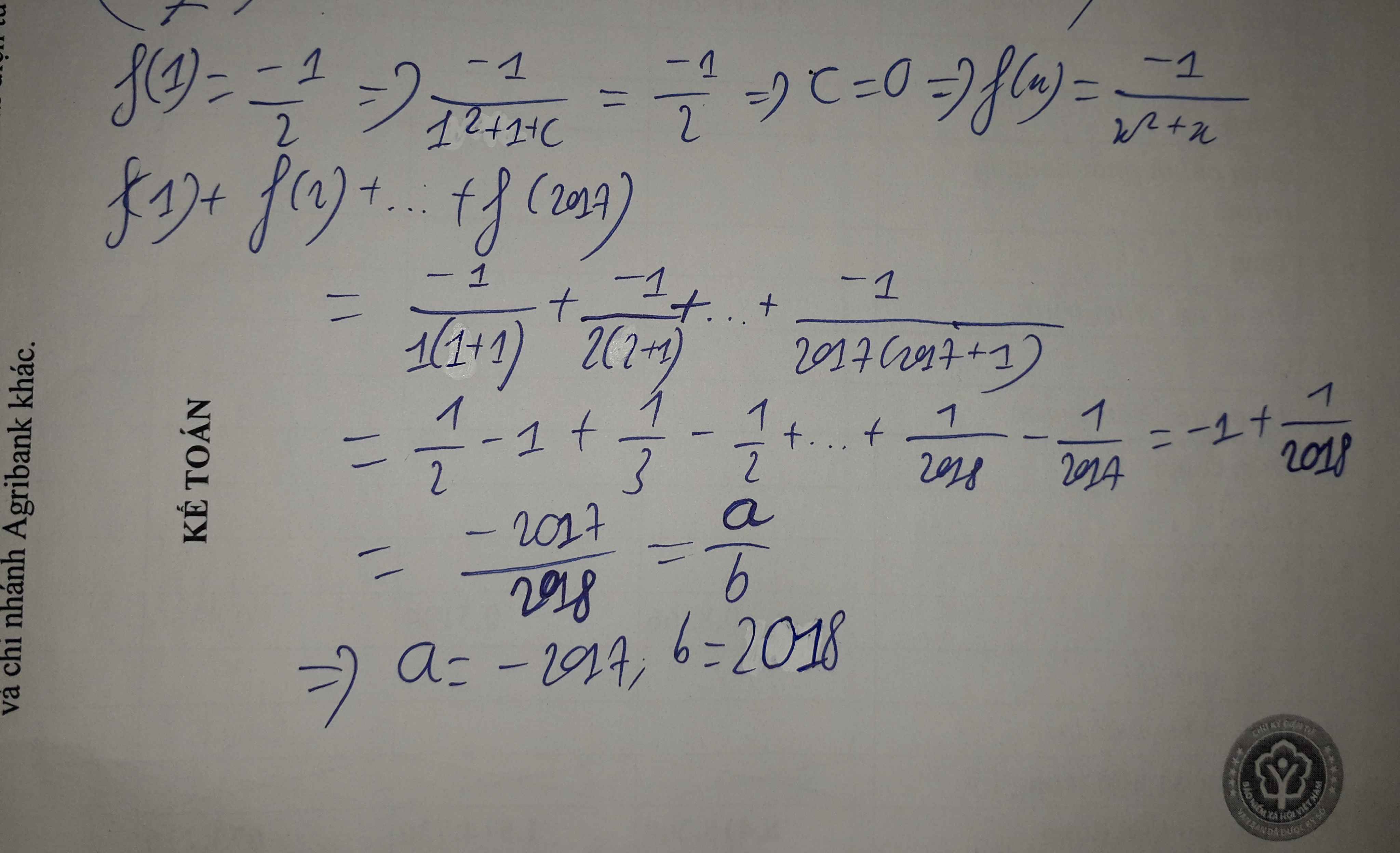

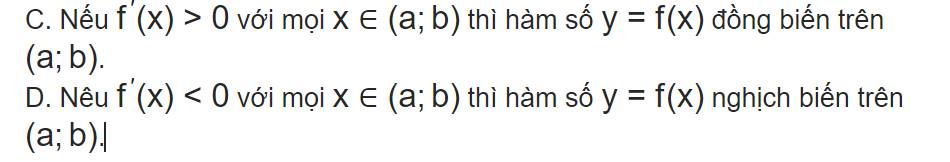
Đáp án C